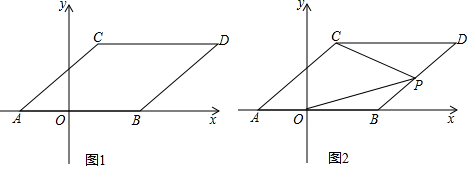题目内容
14.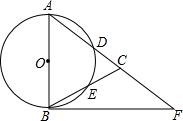 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.点F在AC的延长线上,且∠CBF=$\frac{1}{2}$∠CAB.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.点F在AC的延长线上,且∠CBF=$\frac{1}{2}$∠CAB.(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=$\frac{1}{2}$,求BC和BF的长.
分析 (1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(2)解直角三角形即可得到结论.
解答 (1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴∠1=$\frac{1}{2}$∠CAB.
∵∠CBF=$\frac{1}{2}$∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线;
(2)解:过点C作CG⊥AB于G.
∵sin∠CBF=$\frac{1}{2}$,∠1=∠CBF,
∴sin∠1=$\frac{1}{2}$,
∵在Rt△AEB中,∠AEB=90°,AB=5,
∴BE=AB•sin∠1=5×$\frac{1}{2}$=$\frac{5}{2}$,
∵AB=AC,∠AEB=90°,
∴BC=2BE=5,
∴AB=AC=BC,
∴∠BAC=60°,
∴∠F=30°,
∴BF=$\sqrt{3}$AB=5$\sqrt{3}$.
点评 本题考查了圆的综合题:切线的判定与性质、勾股定理、直角所对的圆周角是直角、解直角三角形等知识点.

练习册系列答案
相关题目
18.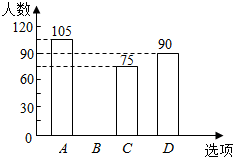 某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
请结合统计图表,回答下列问题:
(1)本次调查的学生共300人,a=10%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.
 某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 朗诵 | 25% |
| D | 器乐 | 30% |
(1)本次调查的学生共300人,a=10%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.
6.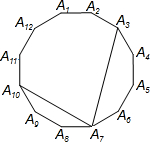 如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10的度数为( )
如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10的度数为( )
 如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10的度数为( )
如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
3.下列因式分解正确的是( )
| A. | a(x+y)=ax+ay | B. | x2+xy+y2=(x+y)2-xy | ||
| C. | 2x2+2y=2(x2+y) | D. | x2-y2=(x-y)2 |
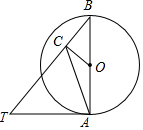 如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
如图,AB是⊙O的直径,∠ABT=45°,AT=AB.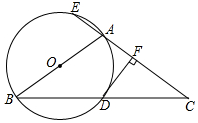 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.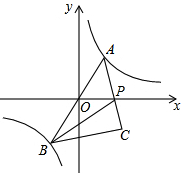 如图,反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2$\sqrt{2}$,-2).
如图,反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2$\sqrt{2}$,-2).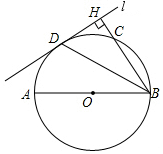 如图,AB为⊙O的直径,直线1切⊙O于点D,过点B作BH⊥1于点H,交⊙O于点C,连接BD.
如图,AB为⊙O的直径,直线1切⊙O于点D,过点B作BH⊥1于点H,交⊙O于点C,连接BD.