题目内容
19．$\sqrt{\frac{y}{x}}$+$\sqrt{\frac{x}{y}}$=$\frac{3\sqrt{2}}{2}$，那么$\frac{y}{x}$+$\frac{x}{y}$的值等于（ ）| A． | $\frac{3}{2}$ | B． | $\frac{5}{2}$ | C． | $\frac{7}{2}$ |
分析 已知等式两边平方，利用完全平方公式化简，整理即可求出$\frac{y}{x}$+$\frac{x}{y}$的值．
解答 解：把$\sqrt{\frac{y}{x}}$+$\sqrt{\frac{x}{y}}$=$\frac{3\sqrt{2}}{2}$，两边平方得：$\frac{y}{x}$+$\frac{x}{y}$+2=$\frac{9}{2}$，
则$\frac{y}{x}$+$\frac{x}{y}$=$\frac{5}{2}$，
故选B
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
优加精卷系列答案
相关题目
10．某纪念币从2013年11月11日起开始上市，通过市场调查得知该纪念币每1枚的市场价y（单位：元）与上市时间x（单位：天）的数据如下：
（1）根据上表数据，在某一特定时期内，可从下列函数中选取一个恰当的函数描述纪念币的市场价y与上市时间x的变化关系：
①y=ax+b（a≠0）； ②y=a（x-h）2+k（ a≠0）； ③y=$\frac{a}{x}$（a≠0）．
你可选择的函数的序号是②．
（2）利用你选取的函数，求该纪念币上市多少天时市场价最低，最低价格是多少？
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
①y=ax+b（a≠0）； ②y=a（x-h）2+k（ a≠0）； ③y=$\frac{a}{x}$（a≠0）．
你可选择的函数的序号是②．
（2）利用你选取的函数，求该纪念币上市多少天时市场价最低，最低价格是多少？
7．若x，y均为非负数，则方程6x=-7y的解的情况是（ ）
| A． | 无解 | B． | 有唯一一个解 | C． | 有无数多个解 | D． | 不能确定 |
14．某中学矩形了一次演讲比赛，分段统计参赛同学的成绩，结果如表所示（分数为整数，满分为100分）：
则这次演讲比赛的同学的平均数为77分～86分．
| 分数段（分） | 61～70 | 71～80 | 81～90 | 91～100 |
| 人数（人） | 2 | 8 | 6 | 4 |
8．
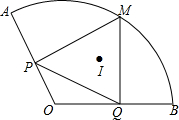如图，扇形AOB的半径为2，∠AOB=120°，点P、Q是半径OA、OB上的动点，M是$\widehat{AB}$上一点，且MP⊥OA于P，MQ⊥OB于Q，I是△MPQ的内心，则MI的长度的范围是（ ）
如图，扇形AOB的半径为2，∠AOB=120°，点P、Q是半径OA、OB上的动点，M是$\widehat{AB}$上一点，且MP⊥OA于P，MQ⊥OB于Q，I是△MPQ的内心，则MI的长度的范围是（ ）| A． | 1≤MI≤$\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$≤MI≤1 | C． | $\frac{1}{2}$≤MI≤$\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$-1≤MI≤1 |
9．下列命题中，真命题是（ ）
| A． | 等边三角形既是轴对称图形又是中心对称图形 | |
| B． | 两条对角线互相垂直且平分的四边形是正方形 | |
| C． | 有一个角是60°的等腰三角形是等边三角形 | |
| D． | 有两条对角线相等的四边形是矩形 |