题目内容
9.先化简,再求值:($\frac{2x}{x-1}$-$\frac{x}{{x}+1}$)÷$\frac{1}{{x}^{2}-1}$,其中x=$\sqrt{2}$-1.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=[$\frac{2x(x+1)}{(x+1)(x-1)}$-$\frac{x(x-1)}{(x+1)(x-1)}$]•(x+1)(x-1)
=x2+2x+1
=(x+1)2,
当x=$\sqrt{2}$-1时,原式=2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11. 将两个长方体如图放置,则所构成的几何体的左视图可能是( )
将两个长方体如图放置,则所构成的几何体的左视图可能是( )
 将两个长方体如图放置,则所构成的几何体的左视图可能是( )
将两个长方体如图放置,则所构成的几何体的左视图可能是( )| A. |  | B. |  | C. |  | D. |  |
4.观察下列图形,阅读图形下面的相关文字,
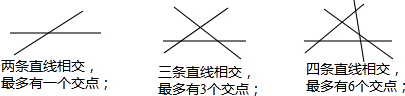
(1)填空
(2)当若干条直线相交时,设最多交点个数为m,对顶角对数为n,则m与n有何关系?

(1)填空
| 直线条数 | 最多交点个数 | 对顶角的对数 |
| 2 | 1 | 2 |
| 3 | 3 | 6 |
| 4 | 6 | 12 |
| 5 | 10 | 20 |
| … | … | … |
| n | $\frac{n(n-1)}{2}$ | n(n-1) |
14.已知:AB⊥CD,垂足为O,EF经过点O,∠AOE=35°,则∠DOF等于( )
| A. | 65° | B. | 55°或125° | C. | 35° | D. | 65°或155° |
1. 如图,△ABC中,CD⊥AB,垂足为D,下列条件中:①∠A+∠B=90°;②AB2=AC2+BC2;③$\frac{AC}{AB}$=$\frac{CD}{BD}$;④CD2=AD•BD,能证明△ABC是直角三角形的有( )
如图,△ABC中,CD⊥AB,垂足为D,下列条件中:①∠A+∠B=90°;②AB2=AC2+BC2;③$\frac{AC}{AB}$=$\frac{CD}{BD}$;④CD2=AD•BD,能证明△ABC是直角三角形的有( )
 如图,△ABC中,CD⊥AB,垂足为D,下列条件中:①∠A+∠B=90°;②AB2=AC2+BC2;③$\frac{AC}{AB}$=$\frac{CD}{BD}$;④CD2=AD•BD,能证明△ABC是直角三角形的有( )
如图,△ABC中,CD⊥AB,垂足为D,下列条件中:①∠A+∠B=90°;②AB2=AC2+BC2;③$\frac{AC}{AB}$=$\frac{CD}{BD}$;④CD2=AD•BD,能证明△ABC是直角三角形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.$\sqrt{\frac{y}{x}}$+$\sqrt{\frac{x}{y}}$=$\frac{3\sqrt{2}}{2}$,那么$\frac{y}{x}$+$\frac{x}{y}$的值等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{7}{2}$ |