题目内容
8.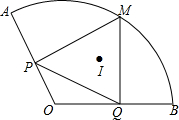 如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )
如图,扇形AOB的半径为2,∠AOB=120°,点P、Q是半径OA、OB上的动点,M是$\widehat{AB}$上一点,且MP⊥OA于P,MQ⊥OB于Q,I是△MPQ的内心,则MI的长度的范围是( )| A. | 1≤MI≤$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$≤MI≤1 | C. | $\frac{1}{2}$≤MI≤$\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$-1≤MI≤1 |
分析 ①当点P,Q分别为OA,OB的中点时,MI有最大值,如图1,连接OM,PI,由∠AOB=120°,OP=OQ,得到∠OPQ=∠OQP=30°,证得△PQM是等边三角形,根据I是△MPQ的内心,求得IM的最大值;
②当P或Q与O重合时,IM有最小值,如图2,过作IE⊥PQ,IF⊥MQ,则四边形IEQF是正方形,根据I是△MPQ的内心,得到IF是内切圆的半径,∠IMQ=30°,由于∠AOB=120°,MP⊥OA得到∠MPQ=30°,根据PM=2,求得PQ=$\sqrt{3}$,MQ=1,得到IF=$\frac{\sqrt{3}-1}{2}$,求出MI最小值.
解答 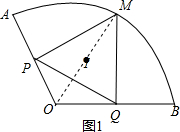 解:①当点P,Q分别为OA,OB的中点时,MI有最大值,
解:①当点P,Q分别为OA,OB的中点时,MI有最大值,
如图1,连接OM,PI,
∵∠AOB=120°,OP=OQ,
∴∠OPQ=∠OQP=30°,
∵MP⊥OA于P,MQ⊥OB于Q,
∴∠MPQ=∠MQP=60°,
∴△PQM是等边三角形,
∵I是△MPQ的内心,
∴OM过点I,
∴IM=OI=$\frac{1}{2}$OM=1;
②当P或Q与O重合时,IM有最小值,如图2,过作IE⊥PQ,IF⊥MQ,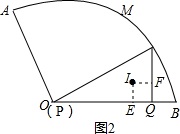
则四边形IEQF是正方形,
∵I是△MPQ的内心,
∴IF是内切圆的半径,∠IMQ=30°,
∴IF=$\frac{1}{2}$(PM+PQ+MQ),
∵∠AOB=120°,MP⊥OA,
∴∠MPQ=30°,
∵PM=2,
∴PQ=$\sqrt{3}$,MQ=1,
∴IF=$\frac{\sqrt{3}-1}{2}$,
∴MI=$\sqrt{3}$-1,
∴MI的长度的范围是:$\sqrt{3}$-1≤IM≤1,
故选D.
点评 本题考查了三角形的内心和内切圆,最值问题,知道三角形内切圆的半径=两直角边的和减去斜边的差的一半是解题的关键.

| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{7}{2}$ |