题目内容
13.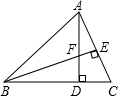 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
分析 (1)由∠C+∠DBF=90°,∠C+∠DAC=90°,推出∠DBF=∠DAC,由此即可证明.
(2)先证明AD=BD,由△ACD∽△BFD,得$\frac{AC}{BF}$=$\frac{AD}{BD}$=1,即可解决问题.
解答 (1)证明: ∵AD⊥BC,BE⊥AC,
∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)∵tan∠ABD=1,∠ADB=90°
∴$\frac{AD}{BD}$=1,
∴AD=BD,
∵△ACD∽△BFD,
∴$\frac{AC}{BF}$=$\frac{AD}{BD}$=1,
∴BF=AC=3.
点评 本题考查相似三角形的判定和性质、三角函数等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{ABC}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{ABC}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{ABC}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{ABC}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
1. 如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是( )
如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是( )
 如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是( )
如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,组成这个几何体的小正方体的个数最少是( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
18.下列运算正确的是( )
| A. | a6÷a2=a3 | B. | (a2)3=a5 | C. | a2•a3=a6 | D. | 3a2-2a2=a2 |
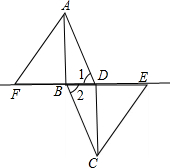 如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.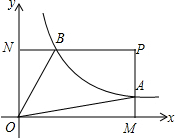 如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=$\frac{k}{x}$的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=6.
如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=$\frac{k}{x}$的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=6. 如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=35度.
如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=35度. 如图,由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,其主视图是( )
如图,由5块完全相同的小正方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,其主视图是( )



 如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=$\sqrt{2}$.
如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=$\sqrt{2}$.