题目内容
15.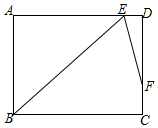 如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=$6\sqrt{2}+3$.(结果保留根号)
如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=$6\sqrt{2}+3$.(结果保留根号)
分析 先延长EF和BC,交于点G,再根据条件可以判断三角形ABE为等腰直角三角形,并求得其斜边BE的长,然后根据条件判断三角形BEG为等腰三角形,最后根据△EFD∽△GFC得出CG与DE的倍数关系,并根据BG=BC+CG进行计算即可.
解答  解:延长EF和BC,交于点G
解:延长EF和BC,交于点G
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=9,
∴直角三角形ABE中,BE=$\sqrt{{9}^{2}+{9}^{2}}$=$9\sqrt{2}$,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE=$9\sqrt{2}$
由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC
∴$\frac{CG}{DE}=\frac{CF}{DF}=\frac{CF}{2CF}=\frac{1}{2}$
设CG=x,DE=2x,则AD=9+2x=BC
∵BG=BC+CG
∴$9\sqrt{2}$=9+2x+x
解得x=$3\sqrt{2}-3$
∴BC=9+2($3\sqrt{2}$-3)=$6\sqrt{2}+3$
故答案为:$6\sqrt{2}+3$
点评 本题主要考查了矩形、相似三角形以及等腰三角形,解决问题的关键是掌握矩形的性质:矩形的四个角都是直角,矩形的对边相等.解题时注意:有两个角对应相等的两个三角形相似.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
5.函数y=$\sqrt{5-x}$自变量x的取值范围是( )
| A. | x>5 | B. | x≥5 | C. | x<5 | D. | x≤5 |
7.$\root{3}{8}$的算术平方根是( )
| A. | 2 | B. | ±2 | C. | $\sqrt{2}$ | D. | $±\sqrt{2}$ |
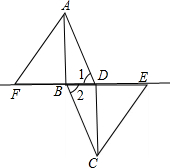 如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.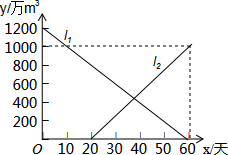 由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素). 如图,直线m∥n,△ABC为等腰直角三角形,∠BAC=90°,则∠1=45度.
如图,直线m∥n,△ABC为等腰直角三角形,∠BAC=90°,则∠1=45度. 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{ABC}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{ABC}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( ) 如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=35度.
如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=35度.