题目内容
16.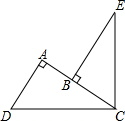 如图,点B在AC上,DC=CE,∠DAC=∠CBE=∠DCE=90°,AD=2,AB=1.求BE的长.
如图,点B在AC上,DC=CE,∠DAC=∠CBE=∠DCE=90°,AD=2,AB=1.求BE的长.
分析 利用同角的余角相等求出∠ACD=∠E,然后利用“角角边”证明△ACD和△BEC全等,根据全等三角形对应边相等可得BC=AD,BE=AC,然后求解即可.
解答 解:∵∠CBE=∠DCE=90°,
∴∠ACD+∠BCE=∠E+∠ACE=90°,
∴∠ACD=∠E,
在△ACD和△BEC中,
$\left\{\begin{array}{l}{∠ACD=∠E}\\{∠DAC=∠CBE=90°}\\{DC=CE}\end{array}\right.$,
∴△ACD≌△BEC(AAS),
∴BC=AD,BE=AC,
∵AD=2,AB=1,
∴AC=AB+BC=AB+AD=1+2=3,
∴BE=3.
点评 本题考查了全等三角形的判定与性质,同角的余角相等的性质,熟练掌握三角形全等的判断方法并准确识图是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
7.-2017的相反数是( )
| A. | -2017 | B. | 2017 | C. | -$\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
1.盒子中装有2个红球和4个绿球,每个球除颜色外完全相同,从盒子中任意摸出一个球,是绿球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
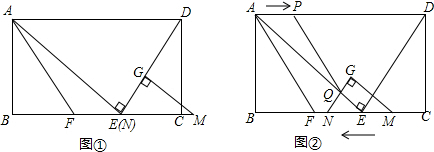
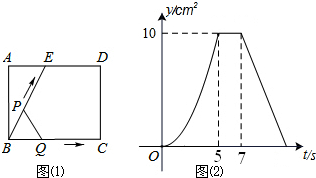 如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图(2),当t=$\frac{29}{4}$秒时,△ABE与△BQP相似.
如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图(2),当t=$\frac{29}{4}$秒时,△ABE与△BQP相似.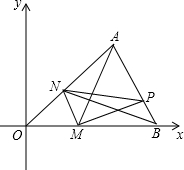 如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.
如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.