题目内容
5.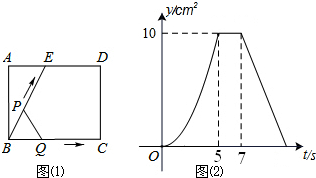 如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图(2),当t=$\frac{29}{4}$秒时,△ABE与△BQP相似.
如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图(2),当t=$\frac{29}{4}$秒时,△ABE与△BQP相似.
分析 先根据图象信息求出AB、BE、BE、AE、ED,再利用相似三角形性质列出方程解决.
解答 解:由图象可知,BC=BE=5,AB=4,AE=3,DE=2,
∵△ABE与△BQP相似,
∴点E只有在CD上,且满足$\frac{BC}{AB}$=$\frac{CQ}{AE}$,
∴$\frac{5}{4}$=$\frac{CQ}{3}$,
∴CQ=$\frac{15}{4}$.
∴t=(BE+ED+DQ)÷1=5+2+(4-$\frac{15}{4}$)=$\frac{29}{4}$.
故答案为$\frac{29}{4}$秒.
点评 本题考查动点问题的函数图象、矩形的性质、三角形的面积公式等知识.解题的关键是读懂图象信息求出相应的线段,学会转化的思想,把问题转化为方程的思想解决,属于中考常考题型.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
14.小红家的收入分农业收入和其他收入两部分,今年农业收入是其他收入的1.5倍,预计明年农业收入将减少20%,而其他收入将增加25%,那么预计小红家明年的全年总收入( )
| A. | 减少2% | B. | 增加2% | C. | 减少0.2% | D. | 增加0.2% |
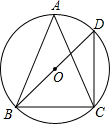 如图,⊙O是△ABC的外接圆,∠A=45°,BD为⊙O的直径,BD=$\sqrt{2}$,连结CD,则CD的长为1.
如图,⊙O是△ABC的外接圆,∠A=45°,BD为⊙O的直径,BD=$\sqrt{2}$,连结CD,则CD的长为1.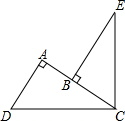 如图,点B在AC上,DC=CE,∠DAC=∠CBE=∠DCE=90°,AD=2,AB=1.求BE的长.
如图,点B在AC上,DC=CE,∠DAC=∠CBE=∠DCE=90°,AD=2,AB=1.求BE的长. 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点. 根据图象直接写出kx+b-$\frac{6}{x}$<0的x的取值范围:0<x<1或x>3.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点. 根据图象直接写出kx+b-$\frac{6}{x}$<0的x的取值范围:0<x<1或x>3.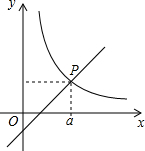 如图,直线y1=x-1与双曲线y2=$\frac{k}{x}$(x>0)交于点P(a,2),则关于x的不等式$\frac{k}{x}$>x-1≥0的解集为1≤x<3.
如图,直线y1=x-1与双曲线y2=$\frac{k}{x}$(x>0)交于点P(a,2),则关于x的不等式$\frac{k}{x}$>x-1≥0的解集为1≤x<3.