��Ŀ����
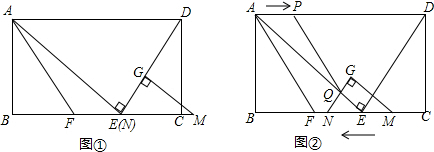
8����֪���ھ���ABCD�У�EΪBC����һ�㣬AE��DE��AB=12��BE=16��FΪ�߶�BE��һ�㣬EF=7������AF����ͼ�٣�����һ��Ӳ��ֽƬ��GMN����NGM=90�㣬NG=6��MG=8��б��MN���BC��ͬһֱ���ϣ���N���E�غϣ���G���߶�DE�ϣ���ͼ�ڣ���GMN��ͼ�ٵ�λ�ó�������ÿ��1����λ���ٶ���EB���B�����ƶ���ͬʱ����P��A���������ÿ��1����λ���ٶ���AD���D�����ƶ�����QΪֱ��GN���߶�AE�Ľ��㣬����PQ������N�����յ�Bʱ����GMN�͵�Pͬʱֹͣ�˶������˶�ʱ��Ϊt�룬����������⣺��1���������˶������У�����G���߶�AE��ʱ����t��ֵ��
��2���������˶������У��Ƿ���ڵ�P��ʹ��APQ�ǵ��������Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ�
��3���������˶������У����GMN���AEF�ص����ֵ����ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ�Լ��Ա���t��ȡֵ��Χ��
���� ��1�����ͼ1��ʾ��֤��QEMGΪƽ���ı��Σ����˶�·��QG=EM=10��tֵ����
��2����APQ�ǵ��������Σ���Ϊ�������Σ���Ҫ�������ۣ�����©�⣮���ͼ2����ͼ3����ͼ4��ʾ��
��3�������˶����̷�Ϊ�ĸ��Σ�ÿ�����ص�ͼ�ε���״������ͬ�����ͼ5-��ͼ8��ʾ���ֱ����������ı���ʽ��
��� 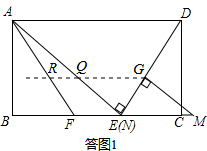 �⣺��1����Rt��GMN�У�GN=6��GM=8����MN=10��
�⣺��1����Rt��GMN�У�GN=6��GM=8����MN=10��
�����⣬��֪��G���˶���·ƽ����BC��
���ͼ1��ʾ������G��BC��ƽ���ߣ��ֱ�AE��AF�ڵ�Q��R��
�ߡ�AED=��EGM=90�㣬��AE��GM��
���ı���QEMGΪƽ���ı��Σ�
��QG=EM=10��
��t=$\frac{10}{1}$=10�룮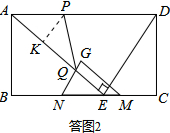
��2�����ڷ��������ĵ�P��
��Rt��ABE�У�AB=12��BE=16���ɹ��ɶ����ã�AE=20��
���AEB=�ȣ���sin��=$\frac{3}{5}$��cos��=$\frac{4}{5}$��
��NE=t����QE=NE•cos��=$\frac{4}{5}$t��AQ=AE-QE=20-$\frac{4}{5}$t��
��APQ�ǵ��������Σ������ֿ��ܵ����Σ�
��AP=PQ�����ͼ2��ʾ��
����P��PK��AE�ڵ�K����AK=AP•cos��=$\frac{4}{5}$t��
��AQ=2AK����20-$\frac{4}{5}$t=2��$\frac{4}{5}$t��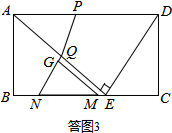
��ã�t=$\frac{25}{3}$��
��AP=AQ�����ͼ3��ʾ��
��t=20-$\frac{4}{5}$t��
��ã�t=$\frac{100}{9}$��
��AQ=PQ�����ͼ4��ʾ��
����Q��QK��AP�ڵ�K����AK=AQ•cos��=��20-$\frac{4}{5}$t����$\frac{4}{5}$=16-$\frac{16}{25}$t��
��AP=2AK����t=2��16-$\frac{16}{25}$t����
��ã�t=$\frac{800}{57}$��
������������t=$\frac{25}{3}$��$\frac{100}{9}$��$\frac{800}{57}$��ʱ�����ڵ�P��ʹ��APQ�ǵ��������Σ�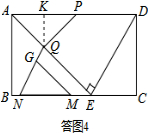
��3�����ͼ1��ʾ����N�����F��ʱ��Ϊt=7��
�ɣ�1��֪����G�����Q��ʱ��Ϊt=10��
QE=10��$\frac{4}{5}$=8��AQ=20-8=12��
��GR��BC����$\frac{QR}{EF}$����$\frac{QR}{7}$����QR=$\frac{21}{5}$��
���G�����R��ʱ��Ϊt=10+$\frac{21}{5}$=$\frac{71}{5}$��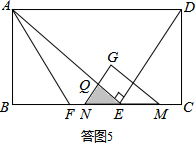
��N�����յ�B��ʱ��Ϊt=16��
���ڡ�GMN�˶��Ĺ����У�
�ٵ�0��t��7ʱ�����ͼ5��ʾ��
QE=NE•cos��=$\frac{4}{5}$t��QN=NE•sin��=$\frac{3}{5}$t��
S=$\frac{1}{2}$QE•QN=$\frac{1}{2}$•$\frac{4}{5}$t•$\frac{3}{5}$t=$\frac{6}{25}$t2��
�ڵ�7��t��10ʱ�����ͼ6��ʾ��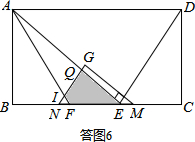
��QN��AF���ڵ�I��
��tan��INF=$\frac{GM}{GN}$=$\frac{4}{3}$��tan��IFN=$\frac{AB}{BF}$=$\frac{4}{3}$��
���INF=��IFN����INF����������
�ױ�NF�ϵĸ�h=$\frac{1}{2}$NF•tan��INF=$\frac{1}{2}$����t-7����$\frac{4}{3}$=$\frac{2}{3}$��t-7����
S��INF=$\frac{1}{2}$NF•h=$\frac{1}{2}$����t-7����$\frac{2}{3}$��t-7��=$\frac{1}{3}$��t-7��2��
��S=S��QNE-S��INF=$\frac{6}{25}$t2-$\frac{1}{3}$��t-7��2=-$\frac{7}{75}$t2+$\frac{14}{3}$t-$\frac{49}{3}$��
�۵�10��t��$\frac{71}{5}$ʱ�����ͼ7��ʾ��
�ɢڵã�S��INF=$\frac{1}{3}$��t-7��2��
��S=S��GMN-S��INF=24-$\frac{1}{3}$��t-7��2=-$\frac{1}{3}$t2+$\frac{14}{3}$t+$\frac{23}{3}$��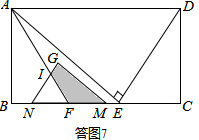
�ܵ�$\frac{71}{5}$��t��16ʱ�����ͼ8��ʾ��
FM=FE-ME=FE-��NE-MN��=17-t��
��GM��AF���ڵ�I������I��IK��MN�ڵ�K��
��tan��IFK=$\frac{AB}{BF}$=$\frac{4}{3}$�������IK=4x��FK=3x����KM=3x+17-t��
��tan��IMF=$\frac{IK}{KM}$=$\frac{4x}{3x+17-t}$=$\frac{3}{4}$����ã�x=$\frac{3}{7}$��17-t����
��IK=4x=$\frac{12}{7}$��17-t����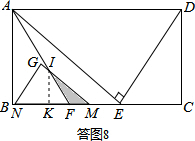
��S=$\frac{1}{2}$FM•IK=$\frac{6}{7}$��t-17��2��
����������S��t֮��ĺ�����ϵʽΪ��
S=$\left\{\begin{array}{l}{\frac{6}{25}{t}^{2}��0��t��7��}\\{-\frac{7}{75}{t}^{2}+\frac{14}{3}t-\frac{49}{3}��7��t��10��}\\{-\frac{1}{3}{t}^{2}+\frac{14}{3}t+\frac{23}{3}��10��t��\frac{71}{5}��}\\{\frac{6}{7}��t-17��^{2}��\frac{71}{5}��t��16��}\end{array}\right.$��
���� ���⿼���˾��ε����ʣ�ƽ���ߵ��ж������ʣ����Ǻ��������ɶ�����ƽ���ı��ε��ж������ʣ�����ؼ����������ͼ�ε��˶����̣�

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{13}{54}$ |
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
| A�� | $\frac{{a}^{2}-{b}^{2}}{��a+b��^{2}}$ | B�� | $\frac{{b}^{2}-{a}^{2}}{a+b}$ | C�� | $\frac{a+b}{a-b}$ | D�� | $\frac{20��a-b��}{15��a+b��}$ |
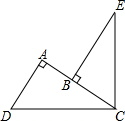 ��ͼ����B��AC�ϣ�DC=CE����DAC=��CBE=��DCE=90�㣬AD=2��AB=1����BE�ij���
��ͼ����B��AC�ϣ�DC=CE����DAC=��CBE=��DCE=90�㣬AD=2��AB=1����BE�ij��� ��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{6}{x}$��x��0����ͼ����A��m��6����B��3��n�����㣮 ����ͼ��ֱ��д��kx+b-$\frac{6}{x}$��0��x��ȡֵ��Χ��0��x��1��x��3��
��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{6}{x}$��x��0����ͼ����A��m��6����B��3��n�����㣮 ����ͼ��ֱ��д��kx+b-$\frac{6}{x}$��0��x��ȡֵ��Χ��0��x��1��x��3��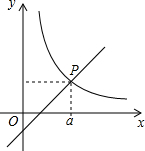 ��ͼ��ֱ��y1=x-1��˫����y2=$\frac{k}{x}$��x��0�����ڵ�P��a��2���������x�IJ���ʽ$\frac{k}{x}$��x-1��0�Ľ⼯Ϊ1��x��3��
��ͼ��ֱ��y1=x-1��˫����y2=$\frac{k}{x}$��x��0�����ڵ�P��a��2���������x�IJ���ʽ$\frac{k}{x}$��x-1��0�Ľ⼯Ϊ1��x��3��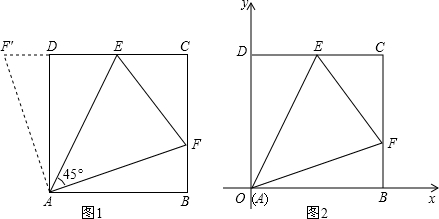
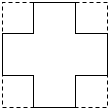 ��ͼ����һ����������Ƭ���ĽǸ���ȥһ���߳�Ϊ3cm��С�����Σ�����һ���ǵĺ��ӣ���֪���ӵ��ݻ�Ϊ300cm3������ԭ��Ƭ�ı߳�Ϊxcm�����������ɵù���x�ķ��̣�x-3��2����x-3��2����3=300��
��ͼ����һ����������Ƭ���ĽǸ���ȥһ���߳�Ϊ3cm��С�����Σ�����һ���ǵĺ��ӣ���֪���ӵ��ݻ�Ϊ300cm3������ԭ��Ƭ�ı߳�Ϊxcm�����������ɵù���x�ķ��̣�x-3��2����x-3��2����3=300��