题目内容
10. 如图,BD、CE为△ABC的两条高,它们的交点为O.
如图,BD、CE为△ABC的两条高,它们的交点为O.(1)请写出与△ABD相似的三角形;
(2)求证:$\frac{OD}{AD}=\frac{OC}{AB}$.
分析 (1)先利用高的定义得到∠BEC=∠BDC=90°,再利用等角的余角相等得到∠ABD=∠ACE,加上∠A=∠A,根据有两组角对应相等的两个三角形相似可判断△ABD∽△ACE,利用同样的方法得到△FBE∽△ABD,△FCD∽△ACE,所以△ABD∽△ACE∽△FBE∽△FCD;
(2)根据相似三角形的性质即可得到结论.
解答 解:(1)∵高BD、CE相交于点O,
∴∠BEC=∠BDC=90°,
∵∠BOE=∠COD,
∴∠ABD=∠ACE,
∵∠A=∠A,
∴△ABD∽△ACE,
∵∠ABD=∠OBE,∠BEO=∠BDA,
∴△OBE∽△ABD,
同理可得△OCD∽△ACE,
∴△ABD∽△ACE∽△OBE∽△OCD;
(2)由(1)证得△ABD∽△OBE∽△OCD,
∴$\frac{OD}{OE}=\frac{OC}{OB}$,①
$\frac{AD}{OE}=\frac{AB}{OB}$ ②,
①÷②得$\frac{OD}{AD}=\frac{OC}{AB}$.
点评 本题考查相似三角形的判定和性质定理,关键是熟记三角形的判定定理,根据定理进行证明求解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
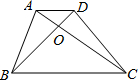 如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?
如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少? 如图,已知线段AB,在线段AB上求作点C,使得AC:BC=2:1.(保留作图痕迹).
如图,已知线段AB,在线段AB上求作点C,使得AC:BC=2:1.(保留作图痕迹).