题目内容
13.一条抛物线的形状、开口方向、对称轴与y=2x2相同,并且抛物线过点(1,1).(1)求抛物线的解析式;
(2)求抛物线的顶点坐标,并说明该抛物线是由抛物线y=2x2经过怎样的平移得到的?
分析 (1)根据抛物线的形状,开口方向、对称轴与y=2x2相同,设出解析式,代入点(1,1),即可求出解析式.
(2)由抛物线的顶点式即可求得顶点坐标,根据左加右减,上加下减可得出答案.
解答 解:(1)根据题意得:设抛物线解析式为y=2x2+k,
∵抛物线过点(1,1),
∴1=2×12+k,
解得k=-1,
∴抛物线的解析式为y=2x2-1.
(2)由y=2x2-1可知抛物线的顶点坐标为(0,-1),
该抛物线是由抛物线y=2x2经过向下平移一个单位得到.
点评 此题考查了待定系数法求二次函数解析式及图象的平移,掌握二次函数的顶点式y=a(x-h)2+k对应的开口方向、对称轴、顶点坐标是解题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
4.一艘轮船从港口A出发向东北方向航行7km,另一艘轮船也从港口A出发向东南方向航行了12km,此时两艘轮船相距( )
| A. | 5km | B. | $\sqrt{193}$km | C. | 19km | D. | 193km |
1.抛物线y=$\frac{1}{2}$(x+2)(x-6)的对称轴是( )
| A. | 直线x=-2 | B. | 直线x=6 | C. | 直线x=2 | D. | 直线x=4 |
5.将a+b-4(a+b)合并同类项,得( )
| A. | 3a+3b | B. | -3a-3b | C. | 4b-3a | D. | 3a-3b |
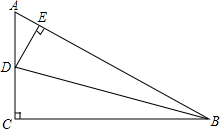 如图,D是△ACB的边AC上一点,AC⊥BC,DE⊥AB,垂足分别为点C,E,∠A=60°,DC=DE,求∠DBC的度数.
如图,D是△ACB的边AC上一点,AC⊥BC,DE⊥AB,垂足分别为点C,E,∠A=60°,DC=DE,求∠DBC的度数.
 如图,BD、CE为△ABC的两条高,它们的交点为O.
如图,BD、CE为△ABC的两条高,它们的交点为O.