题目内容
19.四边形ABCD和四边形A′B′C′D′中,$\frac{AB}{A′B′}=\frac{BC}{B′C′}=\frac{CD}{C′D′}=\frac{DA}{D′A′}=\frac{3}{4}$,且四边形A′B′C′D′的周长为80cm,求四边形ABCD的周长.分析 根据四边形的周长公式和比例的等比性质进行解答.
解答 解:∵$\frac{AB}{A′B′}=\frac{BC}{B′C′}=\frac{CD}{C′D′}=\frac{DA}{D′A′}=\frac{3}{4}$,
∴$\frac{AB+BC+CD+DA}{A′B′+B′C′+C′D′+D′A′}$=$\frac{3}{4}$,
∵A′B′C′D′的周长为80cm,
∴四边形ABCD的周长为60cm.
点评 本题考查的是比例的性质,掌握比例的等比性质是解题的关键.

练习册系列答案
相关题目
9.如果规定符号“?”的意义为a?b=$\frac{a×b}{a+b}$,则2?(-3)的值是( )
| A. | 6 | B. | -6 | C. | $\frac{6}{5}$ | D. | $-\frac{6}{5}$ |
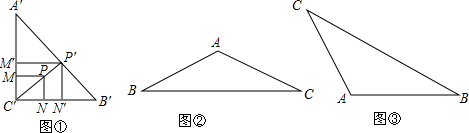
 如图,BD、CE为△ABC的两条高,它们的交点为O.
如图,BD、CE为△ABC的两条高,它们的交点为O. (1)如图,若在象棋上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),那么其他各棋子的坐标分别是什么?
(1)如图,若在象棋上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),那么其他各棋子的坐标分别是什么?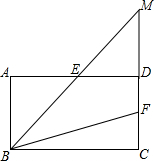 如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.
如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.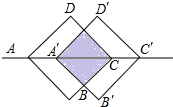 如图所示.正方形ABCD的对角线长为6cm,将此正方形沿对角线AC的方向向右平移2cm得到正方形A′B′C′D′,则平移前后两个图形的重叠部分(阴影部分)的面积为8.
如图所示.正方形ABCD的对角线长为6cm,将此正方形沿对角线AC的方向向右平移2cm得到正方形A′B′C′D′,则平移前后两个图形的重叠部分(阴影部分)的面积为8.