题目内容
2.若数轴上点A、B所代表的数分别为a,b,则A、B两点之间的距离可表示为AB=|a-b|,例如式子|x+1|的几何意义是数轴上表示数x的点与表示数-1的点之间的距离,则满足|x-2|+|x+1|>3的x的取值范围为x>2或x<-1..分析 根据绝对值的意义,可知|x-2|是数轴上表示数x的点与表示数2的点之间的距离,|x+1|是数轴上表示数x的点与表示数-1的点之间的距离,要求|x-2|+|x+1|>3,由线段的性质,两点之间,线段最短,可知当-1≤x≤2时,|x-2|+|x+1|有最小值3,当x>2或x<-1时,|x-2|+|x+1|>3.
解答 解:根据题意,可知当x>2时,|x-2|+|x+1|>3,当x<-1时,|x-2|+|x+1|>3,
故答案为:x>2或x<-1.
点评 本题主要考查的是绝对值的定义的应用,理解并应用绝对值的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.将a+b-4(a+b)合并同类项,得( )
| A. | 3a+3b | B. | -3a-3b | C. | 4b-3a | D. | 3a-3b |
13. 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,BD、CE为△ABC的两条高,它们的交点为O.
如图,BD、CE为△ABC的两条高,它们的交点为O.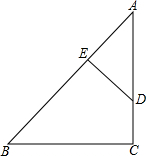 如图,在Rt△ABC中,∠C=90°,DE⊥AB于E,$\frac{AD}{DC}$=$\frac{3}{2}$,AE•AB=15.则AC=5.
如图,在Rt△ABC中,∠C=90°,DE⊥AB于E,$\frac{AD}{DC}$=$\frac{3}{2}$,AE•AB=15.则AC=5. (1)如图,若在象棋上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),那么其他各棋子的坐标分别是什么?
(1)如图,若在象棋上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),那么其他各棋子的坐标分别是什么?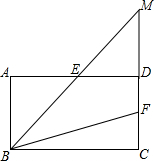 如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.
如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.