题目内容
5.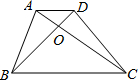 如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?
如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?
分析 根据AD∥BC得到:△AOD∽△COB,可得相似三角形相似比,再利用同高的三角形面积比等于底边比,可求面积比.
解答 解:∵AD∥BC,
∴△AOD∽△COB,
∴OA:OC=AD:BC=OD:OB=1:3
∴S1:S2=OD:OB=1:3
同理,S2:S3=OA:OC=1:3,
∴S1:S2:S3=1:3:9.
点评 本题主要考查了相似三角形的性质和判定,以及同高三角形的面积的比等于底边比,并且考查了三角形的面积的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列各组三条线段中,不能组成三角形的是( )
| A. | a+2,a+2,a+3(a>0) | B. | 3a,5a,2a+1(a>0) | ||
| C. | 三条线段之比为1﹕2﹕3 | D. | 3cm,8cm,10cm |
13. 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
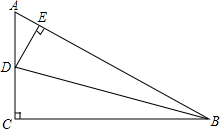 如图,D是△ACB的边AC上一点,AC⊥BC,DE⊥AB,垂足分别为点C,E,∠A=60°,DC=DE,求∠DBC的度数.
如图,D是△ACB的边AC上一点,AC⊥BC,DE⊥AB,垂足分别为点C,E,∠A=60°,DC=DE,求∠DBC的度数.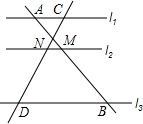 如图,l1∥l2∥l3,AM=2,MB=3,CD=4.5,则ND=2.7,CN=1.8.
如图,l1∥l2∥l3,AM=2,MB=3,CD=4.5,则ND=2.7,CN=1.8. 如图,BD、CE为△ABC的两条高,它们的交点为O.
如图,BD、CE为△ABC的两条高,它们的交点为O.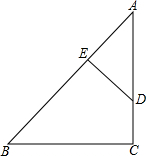 如图,在Rt△ABC中,∠C=90°,DE⊥AB于E,$\frac{AD}{DC}$=$\frac{3}{2}$,AE•AB=15.则AC=5.
如图,在Rt△ABC中,∠C=90°,DE⊥AB于E,$\frac{AD}{DC}$=$\frac{3}{2}$,AE•AB=15.则AC=5.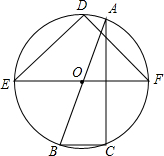 如图,一副三角板ABC和DEF的顶点都在同一个圆上,且EF∥BC,求劣弧DA和劣弧BCF的度数和.
如图,一副三角板ABC和DEF的顶点都在同一个圆上,且EF∥BC,求劣弧DA和劣弧BCF的度数和.