题目内容
已知关于x的分式方程
=1,下列说法中正确的是( )
| 2m |
| x+6 |
| A、该方程的解是x=2m-6 |
| B、m<3时,该方程的解为负数 |
| C、m>3时,该方程的解为正数 |
| D、m≠3时,该方程无解 |
考点:分式方程的解
专题:
分析:先将分式方程化成整式方程用含m的式子表示x,然后根据x+6≠0进行分析即可.
解答:解:
=1,
去分母化成整式方程得:2m=x+6,
所以x=2m-6,
但是x+6≠0,
所以x≠-6,
即2m-6≠-6,
所以m≠0,
所以当m≠0时,该方程的解是x=2m-6,故A错误;
当m=0时,该方程无解,故D错误;
当x>0时,即2m-6>0,解得:m>3,
即m>3时,该方程的解为正数,故C正确;
当x<0时,即2m-6<0,解得:m<3,
即m<3,且m≠0时,该方程的解为负数,故B错误.
故选:C.
| 2m |
| x+6 |
去分母化成整式方程得:2m=x+6,
所以x=2m-6,
但是x+6≠0,
所以x≠-6,
即2m-6≠-6,
所以m≠0,
所以当m≠0时,该方程的解是x=2m-6,故A错误;
当m=0时,该方程无解,故D错误;
当x>0时,即2m-6>0,解得:m>3,
即m>3时,该方程的解为正数,故C正确;
当x<0时,即2m-6<0,解得:m<3,
即m<3,且m≠0时,该方程的解为负数,故B错误.
故选:C.
点评:此题考查了分式方程的解,解题的关键是:考虑增根的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知△ABC是等边三角形,则∠BDC=( )
如图,已知△ABC是等边三角形,则∠BDC=( )| A、30° | B、60° |
| C、90° | D、120° |
袋中有4个除颜色外其余都相同的小球,其中1个红色,1个黑色,2个白色.现随机从袋中摸取两个球,则摸出的球都是白色的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
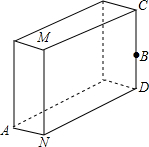 如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少?
如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少?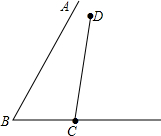 先填空,后作图:
先填空,后作图: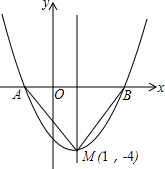 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)