题目内容
适合下列条件的△ABC中,直角三角形的个数为( )
①∠A:∠B:∠C=1:2:3;②a=6,b=6,∠A=45°;③∠A=32°,∠B=58°;④a=7,b=24,c=25;⑤a=2,b=2,c=4.
①∠A:∠B:∠C=1:2:3;②a=6,b=6,∠A=45°;③∠A=32°,∠B=58°;④a=7,b=24,c=25;⑤a=2,b=2,c=4.
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:勾股定理的逆定理,三角形内角和定理
专题:
分析:先根据三角形的内角和是180°对①②③中△ABC的形状作出判断,再根据勾股定理的逆定理对④⑤中△ABC的形状进行判断即可.
解答:解:①∵△ABC中,∠A:∠B:∠C=1:2:3,
∴设∠A=x,则∠B=2x,∠C=3x,
∵∠A+∠B+∠C=180°,
∴x+2x+3x=180°,解得x=30°,
∴∠C=3x=2×30°=90°,
∴△ABC是直角三角形,故本小题正确;
②∵△ABC中,a=6,b=6,
∴∠B=∠A=45°,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本小题正确;
③∵△ABC中,∠A=32°,∠B=58°,且∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本小题正确;
④∵△ABC中,a=7,b=24,c=25,
∴c2=a2+b2,
∴△ABC为直角三角形,故本小题正确;
⑤∵△ABC中,a=2,b=2,c=4,
∴c2≠a2+b2,
∴△ABC不是直角三角形,故本小题错误.
∴是直角三角形的有①②③④.
故选C.
∴设∠A=x,则∠B=2x,∠C=3x,
∵∠A+∠B+∠C=180°,
∴x+2x+3x=180°,解得x=30°,
∴∠C=3x=2×30°=90°,
∴△ABC是直角三角形,故本小题正确;
②∵△ABC中,a=6,b=6,
∴∠B=∠A=45°,
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本小题正确;
③∵△ABC中,∠A=32°,∠B=58°,且∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本小题正确;
④∵△ABC中,a=7,b=24,c=25,
∴c2=a2+b2,
∴△ABC为直角三角形,故本小题正确;
⑤∵△ABC中,a=2,b=2,c=4,
∴c2≠a2+b2,
∴△ABC不是直角三角形,故本小题错误.
∴是直角三角形的有①②③④.
故选C.
点评:本题考查的是三角形内角和定理及勾股定理的逆定理,解答此题的关键是利用方程的思想把△ABC中的边角关系转化为求x的值,再根据直角三角形的性质进行判断.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
袋中有4个除颜色外其余都相同的小球,其中1个红色,1个黑色,2个白色.现随机从袋中摸取两个球,则摸出的球都是白色的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在⊙O中,
如图,在⊙O中, |
| AD |
 |
| BC |
| A、70° | B、35° |
| C、60° | D、30° |
本学期的五次数学测试中,甲、乙两同学的平均成绩一样,方差分别为1.3、0.4,由此可知( )
| A、甲比乙的成绩稳定 |
| B、乙比甲的成绩稳定 |
| C、甲乙两人的成绩一样稳定 |
| D、无法确定谁的成绩更稳定 |
设A(-1,y1)、B(1,y2)、C(3,y3)是抛物线y=-
(x-
)2+k上的三个点,则y1、y2、y3的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y2<y3<y1 |
下列方程组是二元一次方程组的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
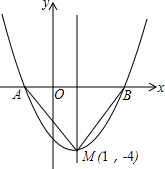 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)