题目内容
2.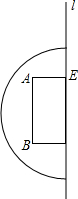 如图,是一幅关于直线l对称的不完整图案,其中的曲线是半圆,∠A=∠B=90°,AB∥l,
如图,是一幅关于直线l对称的不完整图案,其中的曲线是半圆,∠A=∠B=90°,AB∥l,(1)将其补成完整的图案(保留画图痕迹);
(2)若AE=$\frac{1}{2}$AB,在平面直角坐标系中,l与y轴重合,点A的坐标(-2,4),则点A关于l的对称点坐标为(2,4),点B关于l的对称点坐标为(2,0).
分析 (1)利用轴对称图形的性质得出直线l的右边部分即可;
(2)利用已知点的坐标结合轴对称的性质,得出对应点坐标即可.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)∵AE=$\frac{1}{2}$AB,在平面直角坐标系中,l与y轴重合,点A的坐标(-2,4),
∴点A关于l的对称点坐标为:(2,4),点B关于l的对称点坐标为:(2,0).
故答案为:(2,4),(2,0).
点评 此题主要考查了利用轴对称设计图案以及坐标性质,利用轴对称的性质得出是解题关键.

练习册系列答案
相关题目
10.下列各式中运算正确的式子是( )
| A. | a3•a2=a6 | B. | (-a3)2=a5 | C. | $-\sqrt{{{({-3})}^2}}=-3$ | D. | ${(-1)^{-2}}=\frac{1}{2}$ |
17.计算$\frac{\sqrt{8}}{\sqrt{12}}÷\sqrt{\frac{45}{12}}×\sqrt{\frac{5}{8}}$的值是( )
| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{3\sqrt{3}}{4}$ |
 如图,△ABC绕点A逆时针旋转60°到△ADE的位置,点B的对应点是点D,点C的对应点是点E,已知∠BAC=125°,则∠DAC等于65°.
如图,△ABC绕点A逆时针旋转60°到△ADE的位置,点B的对应点是点D,点C的对应点是点E,已知∠BAC=125°,则∠DAC等于65°.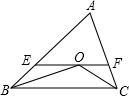 已知:如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的平分线交于点O,过点O作EF∥BC交AB于E,交AC于F.求∠BOC的度数.
已知:如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的平分线交于点O,过点O作EF∥BC交AB于E,交AC于F.求∠BOC的度数. 如图,BD平分∠ABC,ED∥BC,∠1=25°,∠4=130°.
如图,BD平分∠ABC,ED∥BC,∠1=25°,∠4=130°.