题目内容
14.已知y与x+2成反比例,且当x=5时,y=-6,求:(1)y与x之间的函数关系式;
(2)当y=5时,x的值.
分析 (1)根据y与x+2成反比例设y与x之间的函数关系式为:y=$\frac{k}{x+2}$,将一对x、y的值代入利用待定系数法确定函数关系式即可.
(2)令y=3求得x的值即可.
解答 解:(1)设y与x之间的函数关系式为:y=$\frac{k}{x+2}$,
由题意得:-6=$\frac{k}{5+2}$,
∴k=-42,
∴y=-$\frac{42}{x+2}$;
(2)当y=5时,-$\frac{42}{x+2}$=5,解得x=-$\frac{52}{5}$.
经检验:x=-$\frac{52}{5}$是-$\frac{42}{x+2}$=5的解,所以当y=5时,x=-$\frac{52}{5}$.
点评 本题考查了待定系数法确定反比例函数的解析式的知识,解题的关键是根据题意设出待定系数,难点较小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,在△ABC中,D、E分别是边AB和AC的中点,BC=4,下面结论中不正确的是( )
如图,在△ABC中,D、E分别是边AB和AC的中点,BC=4,下面结论中不正确的是( )
 如图,在△ABC中,D、E分别是边AB和AC的中点,BC=4,下面结论中不正确的是( )
如图,在△ABC中,D、E分别是边AB和AC的中点,BC=4,下面结论中不正确的是( )| A. | DE=2 | |
| B. | △ADE的面积与△ABC的面积之比为1:4 | |
| C. | △ADE∽△ABC | |
| D. | △DEC的周长与△ABC的周长之比为1:2 |
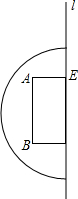 如图,是一幅关于直线l对称的不完整图案,其中的曲线是半圆,∠A=∠B=90°,AB∥l,
如图,是一幅关于直线l对称的不完整图案,其中的曲线是半圆,∠A=∠B=90°,AB∥l, 如图,在?ABCD中,AD⊥BD,点E、F分别在AB、BD上且满足AD=AE=DF,连接DE、AF、EF.
如图,在?ABCD中,AD⊥BD,点E、F分别在AB、BD上且满足AD=AE=DF,连接DE、AF、EF. 如图,正方形ABCD的对角线相交于点O,点E,F分别在OA,OB上,且OE=OF,BE和CF有特殊的大小关系吗?BE和CF有特殊的位置关系吗?证明你的结论.
如图,正方形ABCD的对角线相交于点O,点E,F分别在OA,OB上,且OE=OF,BE和CF有特殊的大小关系吗?BE和CF有特殊的位置关系吗?证明你的结论.