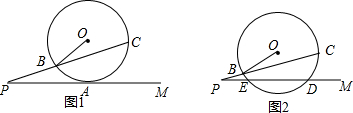题目内容
10.计算:(1)3$\sqrt{48}$-9$\sqrt{\frac{1}{3}}$+3$\sqrt{12}$(2)($\sqrt{4}$+$\sqrt{12}$)(2-2$\sqrt{3}$)-($\sqrt{3}$-$\sqrt{2}$)2.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用平方差公式和完全平方公式计算.
解答 解:(1)原式=12$\sqrt{3}$-3$\sqrt{3}$+6$\sqrt{3}$
=15$\sqrt{3}$;
(2)原式=(2+2$\sqrt{3}$)(2-2$\sqrt{3}$)-(3-2$\sqrt{6}$+2)
=4-12-5+2$\sqrt{6}$
=-13+2$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
5.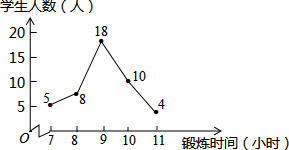 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 9,9 | C. | 9,10 | D. | 18,9 |
15.下列命题:①两条直线被第三条直线所截,同位角相等;②平面内一条直线和两条平行线中的一条相交,则它与另一条也相交;③一条直线只有一条垂线;④从直线外一点到这条直线的垂直线段,叫做这点到直线的距离,其中真命题的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
2.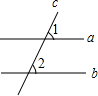 如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
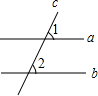 如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
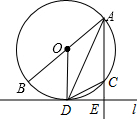 如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.
如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.