题目内容
12.已知有序数组(a,b,c,d),现按下列方式重新写成数组(a1,b1,c1,d1),(a2,b2,c2,d2),使a1=a+b,b1=b+c,c1=c+d,d1=d+a,a2=a1+b1,b2=b1+c1,c2=c1+d1,d2=d1+a1…按照这样的规律继续写出(a3,b3,c3,d3),(a4,b4,c4,d4)…,(an,bn,cn,dn),若$1000<\frac{{{a_n}+{b_n}+{c_n}+{d_n}}}{a+b+c+d}<2000$,则n=( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 分析可得:a1=a+b,b1=b+c,c1=c+d,d1=d+a,则a1+b1+c1+d1=2b+2d+2c+2a,进而的a2+b2+c2+d2=4(a+b+c+d),a3+b3+c3+d3=23(a+b+c+d),…an+bn+cn+dn=2n(a+b+c+d);若$1000<\frac{{{a_n}+{b_n}+{c_n}+{d_n}}}{a+b+c+d}<2000$,即1000<2n<2000,则n=10.
解答 解:an+bn+cn+dn=2n(a+b+c+d)
若$1000<\frac{{{a_n}+{b_n}+{c_n}+{d_n}}}{a+b+c+d}<2000$,
即1000<2n<2000
则n=10.
故选B.
点评 本题考查学生分析数据,总结、归纳数据规律的能力,要求学生要有一定的解题技巧.根据题中所给的材料获取所需的信息和解题方法是需要掌握的基本技能.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
7.小明有一个呈等腰三角形的积木盒,现在积木盒中只剩下如图的九个空格,下面有四种积木的搭配,其中恰好能放入的有( )
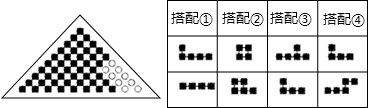

| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
2. 如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
 如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )| A. | 4$\sqrt{3}$π | B. | 4$\sqrt{2}$π | C. | 2$\sqrt{3}$π | D. | 4π |
 作图题(作图工具不限,保留作图痕迹,写出结论)
作图题(作图工具不限,保留作图痕迹,写出结论)