题目内容
2. 如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )| A. | 4$\sqrt{3}$π | B. | 4$\sqrt{2}$π | C. | 2$\sqrt{3}$π | D. | 4π |
分析 首先延长BE交⊙O于点D,连接AD,进而得出△DAE∽△FOE,再求出AD的长,即可得出∠DBA的度数,进而利用弧长公式求出即可.
解答  解:延长BE交⊙O于点D,连接AD,
解:延长BE交⊙O于点D,连接AD,
由题意可得:∠DAB=90°,
又∵FG⊥AB,
∴AD∥FG,
∴△DAE∽△FOE,
∴$\frac{EO}{DE}$=$\frac{FO}{AD}$,
∵⊙O的半径为12,且OE:OF:OB=2:3:6,
∴EO=4,FO=6,DE=8,
∴$\frac{4}{8}$=$\frac{6}{AD}$,
解得:AD=12,
∵BD=24,
∴∠OBA=30°,
∴∠BOG=60°,
∴弧BG的长为:$\frac{60π×12}{180}$=4π.
故选:D.
点评 此题主要考查了相似三角形的判定与性质以及弧长公式的应用以及圆周角定理等知识,得出∠OBA的度数是解题关键.

练习册系列答案
相关题目
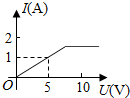
10.某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长成正比例,在营销过程中得到了表格中的数据.
(1)求一张薄板的出厂价与边长之间满足的函数关系式;
(2)40cm的薄板,获得的利润是26元(利润=出厂价-成本价).
①求一张薄板的利润与边长之间满足的函数关系式;
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
(2)40cm的薄板,获得的利润是26元(利润=出厂价-成本价).
①求一张薄板的利润与边长之间满足的函数关系式;
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?
7.邻居王阿姨在再就业中心的扶持下,创办了“便民”报刊零售点,对经营的某种晚报,王阿姨提供了如下信息:
①买进报纸每份0.35元,卖出每份0.5元;
②一个月内(以30天计),有22天每天可以卖出250份,其余每天只能卖出150份;
③一个月内,每天从报社买进的报纸份数必须相同,当天卖剩下的报纸可以每份0.25元退回报社.
根据上述信息,请你给王阿姨帮个忙:
(1)填表:
(2)设每天从报社买进该晚报x份(150≤x≤250)时,月利润为y元,试求出y关于x的函数关系式,并求月利润的最大值.
①买进报纸每份0.35元,卖出每份0.5元;
②一个月内(以30天计),有22天每天可以卖出250份,其余每天只能卖出150份;
③一个月内,每天从报社买进的报纸份数必须相同,当天卖剩下的报纸可以每份0.25元退回报社.
根据上述信息,请你给王阿姨帮个忙:
(1)填表:
| 一个月内每天买进该晚报(份) | 150 | 200 |
| 当月利润(元) | 675 | 800 |

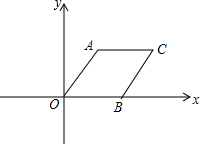 平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.
平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.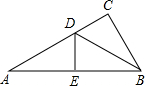 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.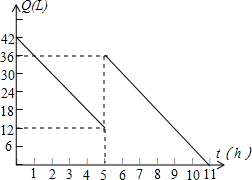 机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数如图,根据图回答问题.
机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数如图,根据图回答问题. 已知,线段a,c和∠β(如图),利用直尺和圆规作△ABC,使BC=a,AB=c,∠ABC=∠β(不写作法,保留作图痕迹)
已知,线段a,c和∠β(如图),利用直尺和圆规作△ABC,使BC=a,AB=c,∠ABC=∠β(不写作法,保留作图痕迹)