题目内容
2.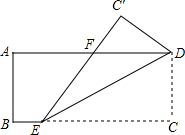 如图,已知矩形ABCD中,AB=4,E是BC上一点,将△CDE沿直线DE折叠后,点C落在点C′处,连接C′E交AD于点F,若BE=2,F为AD的中点,则AD的长为10.
如图,已知矩形ABCD中,AB=4,E是BC上一点,将△CDE沿直线DE折叠后,点C落在点C′处,连接C′E交AD于点F,若BE=2,F为AD的中点,则AD的长为10.
分析 设AD=x,根据线段中点的性质得到DF=$\frac{1}{2}$x,根据矩形的性质和翻折变换的性质得到FE=FD,C′D=CD,根据勾股定理列出关于x的方程,解方程即可.
解答 解:设AD=x,
∵F为AD的中点,
∴DF=$\frac{1}{2}$AD=$\frac{1}{2}$x,
∵AD∥BC,
∴∠DEC=∠FDE,又∠FED=∠DEC,
∴∠FED=∠FDE,
∴FE=DF=$\frac{1}{2}$x,
由翻折变换的性质可知,EC′=EC=x-2,C′D=CD=4,
∴C′F=x-2-$\frac{1}{2}$x=$\frac{1}{2}$x-2,
由勾股定理得,C′F2+C′D2=DF2,即($\frac{1}{2}$x-2)2+42=($\frac{1}{2}$x)2,
解得,x=10,
∴AD的长为10.
故答案为:10.
点评 本题考查的是翻折变换的性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
17.将二次函数y=x2-4的图象先向右平移2个单位,再向上平移3个单位后得到的抛物线的函数表达式为( )
| A. | y=(x+2)2-7 | B. | y=(x-2)2-7 | C. | y=(x+2)2-1 | D. | y=(x-2)2-1 |
14.对于抛物线y=-3(x-2)2+1,下列说法中错误的是( )
| A. | 抛物线开口向下 | B. | 对称轴是直线x=2 | ||
| C. | 顶点坐标是(2,1) | D. | 抛物线与x轴没有交点 |
 如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.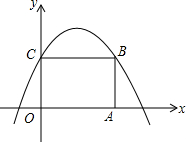 如图,矩形ABCD的顶点A、C分别在x轴、y轴上,点B在第一象限,若函数y=ax2-2ax+1的图象经过点B、C,则点B的坐标是(2,1).
如图,矩形ABCD的顶点A、C分别在x轴、y轴上,点B在第一象限,若函数y=ax2-2ax+1的图象经过点B、C,则点B的坐标是(2,1).


