题目内容
11.解方程:(1)$\frac{x}{{x}^{2}-4}$+$\frac{2}{x+2}$=$\frac{1}{x-2}$
(2)$\frac{4}{2x+1}$=$\frac{x}{2x+1}$+1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x+2(x-2)=x+2,
去括号得:x+2x-4=x+2,
移项合并得:2x=6,
解得:x=3,
经检验x=3是分式方程的解;
(2)方程两边同乘(2x+1),得4=x+2x+1,
解得:x=1,
经检验x=1是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
1.利用平方根、立方根来解下列方程.
(1)(2x-1)2-169=0;
(2)4(3x+1)2-1=0;
(3)$\frac{27}{4}$x3-2=0;
(4)$\frac{1}{2}$(x+3)3=4.
(1)(2x-1)2-169=0;
(2)4(3x+1)2-1=0;
(3)$\frac{27}{4}$x3-2=0;
(4)$\frac{1}{2}$(x+3)3=4.
16. 如图,AB是⊙的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
如图,AB是⊙的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
 如图,AB是⊙的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
如图,AB是⊙的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )| A. | CM=DM | B. | OM=BM | C. | ∠ACD=∠ADC | D. | CB=BD |
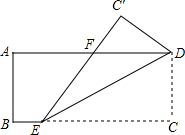 如图,已知矩形ABCD中,AB=4,E是BC上一点,将△CDE沿直线DE折叠后,点C落在点C′处,连接C′E交AD于点F,若BE=2,F为AD的中点,则AD的长为10.
如图,已知矩形ABCD中,AB=4,E是BC上一点,将△CDE沿直线DE折叠后,点C落在点C′处,连接C′E交AD于点F,若BE=2,F为AD的中点,则AD的长为10. 如图,在△ABC中,∠A=62°,点O是AB,AC的垂直平分线的交点,则∠OCB的度数为28°.
如图,在△ABC中,∠A=62°,点O是AB,AC的垂直平分线的交点,则∠OCB的度数为28°. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6cm,AB=8cm,BC=14cm.动点P、Q都从点C同时出发,点P沿C→B方向做匀速运动,点Q沿C→D→A方向做匀速运动,当P、Q其中一点到达终点时,另一点也随之停止运动.若点P以1cm/s速度运动,点Q以2$\sqrt{2}$cm/s的速度运动,连接BQ、PQ.当时间t为2秒时,△BQP的面积为24cm2.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6cm,AB=8cm,BC=14cm.动点P、Q都从点C同时出发,点P沿C→B方向做匀速运动,点Q沿C→D→A方向做匀速运动,当P、Q其中一点到达终点时,另一点也随之停止运动.若点P以1cm/s速度运动,点Q以2$\sqrt{2}$cm/s的速度运动,连接BQ、PQ.当时间t为2秒时,△BQP的面积为24cm2.