将二次函数y=x2-4的图象先向右平移2个单位.再向上平移3个单位后得到的抛物线的函数表达式为( )A．y=(x+2)2-7B．y=(x-2)2-7C．y=(x+2)2-1D．y=(x-2)2-1 题目和参考答案——青夏教育精英家教网—

题目内容

17．将二次函数y=x²-4的图象先向右平移2个单位，再向上平移3个单位后得到的抛物线的函数表达式为（　　）

A．

y=（x+2）²-7

B．

y=（x-2）²-7

C．

y=（x+2）²-1

D．

y=（x-2）²-1

分析由抛物线平移不改变二次项系数a的值，根据点的平移规律“左减右加，上加下减”可知移动后的顶点坐标，再由顶点式可求移动后的函数表达式．

解答解：原抛物线的顶点为（0，-4），向右平移2个单位，再向上平移3个单位后，那么新抛物线的顶点为：（2，-1）．
可设新抛物线的解析式为y=（x-h）²+k，代入得y=（x-2）²-1．
故选D．

点评本题考查了二次函数图象与几何变换．解决本题的关键是得到新抛物线的顶点坐标．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

8．如图，由大小相同的小立方块搭成的几何体．

（1）填空：图中共有5个小立方体．
（2）画出这个几何体的三个视图．

5．下列命题正确的是（　　）

	A．	三点确定一个圆
	B．	平分弦的直径垂直于弦
	C．	等圆中相等的圆心角所对的弧相等
	D．	圆周角的度数等于圆心角度数的一半

12．

如图，在边长为1的正方形组成的网格中，点A、B、C都在格点上，将△ABC绕点A按逆时针方向旋转90°，得到△AB′C′．
（1）画出旋转后的△AB′C′；
（2）求边AB在旋转过程中扫过的面积．

2．

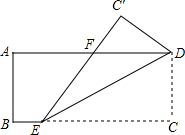如图，已知矩形ABCD中，AB=4，E是BC上一点，将△CDE沿直线DE折叠后，点C落在点C′处，连接C′E交AD于点F，若BE=2，F为AD的中点，则AD的长为10．

9．直线y=kx-3经过点A（-1，-1），求关于x的不等式kx-3≥0的解集．

6．计算：|-3|-2tan45°+（-$\sqrt{2}$）⁰-${（{\frac{1}{3}}）^{-1}}$．

7．已知点P（x，3-x）关于x轴对称的点在第三象限，则x的取值范围是（　　）

试题分类