题目内容
10．
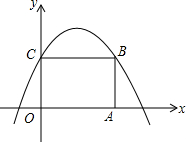如图，矩形ABCD的顶点A、C分别在x轴、y轴上，点B在第一象限，若函数y=ax2-2ax+1的图象经过点B、C，则点B的坐标是（2，1）．
分析 根据解析式求得C的坐标，然后根据矩形的性质把y=1代入y=ax2-2ax+1，解方程即可求得．
解答 解：由函数y=ax2-2ax+1可知C（0，1），
把y=1，代入函数y=ax2-2ax+1得ax2-2ax+1=1，
解得x=0或x=2，
∴B（2，1），
故答案为（2，1）．
点评 本题考查了二次函数图象上点的坐标特征，求得C的坐标在解题的关键．
练习册系列答案
相关题目
20．某班实行小组量化考核制．为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到数据制成如下的统计表：
（1）请根据表中的数据计算甲组与乙组的平均数、中位数、方差．（注：方差的计算结果精确到0.1）
（2）请你分别对甲、乙两个小组连续六周的学习情况作出简要评价．
| 一 | 二 | 三 | 四 | 五 | 六 | |
| 甲 | 12 | 15 | 16 | 14 | 14 | 13 |
| 乙 | 9 | 14 | 10 | 17 | 16 | 18 |
（2）请你分别对甲、乙两个小组连续六周的学习情况作出简要评价．
1．利用平方根、立方根来解下列方程．
（1）（2x-1）2-169=0；
（2）4（3x+1）2-1=0；
（3）$\frac{27}{4}$x3-2=0；
（4）$\frac{1}{2}$（x+3）3=4．
（1）（2x-1）2-169=0；
（2）4（3x+1）2-1=0；
（3）$\frac{27}{4}$x3-2=0；
（4）$\frac{1}{2}$（x+3）3=4．
5．下列命题正确的是（ ）
| A． | 三点确定一个圆 | |
| B． | 平分弦的直径垂直于弦 | |
| C． | 等圆中相等的圆心角所对的弧相等 | |
| D． | 圆周角的度数等于圆心角度数的一半 |
15．已知点A（1，2）、B（-1，b）是反比例函数y=$\frac{k}{x}$图象上的一点，则b的值为（ ）
| A． | -2 | B． | 2 | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
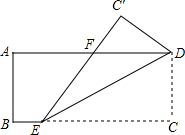如图，已知矩形ABCD中，AB=4，E是BC上一点，将△CDE沿直线DE折叠后，点C落在点C′处，连接C′E交AD于点F，若BE=2，F为AD的中点，则AD的长为10．