题目内容
7.(1)如图1、2,试研究其中∠1、∠2与∠3、∠4之间的数量关系;(2)用你发现的结论解决下列问题:
如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

分析 (1)根据四边形的内角和等于360°用∠5+∠6表示出∠3+∠4,再根据平角的定义用∠5+∠6表示出∠1+∠2,即可得解;
(2)从外角的定义考虑解答;
(3)根据(1)的结论求出∠MDA+∠NAD,再根据角平分线的定义求出∠ADE+∠DAE,然后利用三角形的内角和定理列式进行计算即可得解.
解答 (1)解:∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4;
(2)答:四边形的任意两个外角的和等于与它们不相邻的两个内角的和;
(3)解:∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°,
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=$\frac{1}{2}$∠MDA,∠DAE=$\frac{1}{2}$∠NAD,
∴∠ADE+∠DAE=$\frac{1}{2}$(∠MDA+∠NAD)=$\frac{1}{2}$×240°=120°,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
点评 本题考查了多边形的内角和公式,平角的定义,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
12.若正数m,n满足m2+n2=10,mn=3,则m+n=( )
| A. | ±4 | B. | 4 | C. | -4 | D. | ±16 |
19.计算:
(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
16.在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
(1)表中a的值等于0.25;
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 |
| 摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
| 摸到黑球的频率 $\frac{m}{n}$ | 0.26 | 0.247 | 0.245 | 0.248 | a |
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
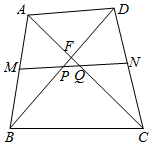 如图,四边形ABCD的对角线AC,BD相交于点F,M,N分别为AB,CD的中点,连接MN分别交BD,AC于点P,Q,且∠FPQ=∠FQP,若BD=9,则AC=9.
如图,四边形ABCD的对角线AC,BD相交于点F,M,N分别为AB,CD的中点,连接MN分别交BD,AC于点P,Q,且∠FPQ=∠FQP,若BD=9,则AC=9. 篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答:
篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答: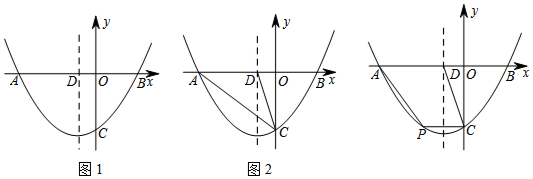
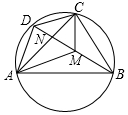 已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证:
已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证: