题目内容
16.在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.| 摸球的次数n | 100 | 150 | 200 | 500 | 800 |
| 摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
| 摸到黑球的频率 $\frac{m}{n}$ | 0.26 | 0.247 | 0.245 | 0.248 | a |
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
分析 (1)直接利用频数÷总数=频率求出答案;
(2)直接利用表格中数据估算出得到白球的频率,进而得出答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次都摸到白球的情况,再利用概率公式即可求得答案.
解答 解:(1)由题意可得:a=200÷800=0.25;
故答案为:0.25;
(2)又表格中数据可得出,摸到黑球的频率稳定在0.25,
故1÷0.25-1=3(个),
答:口袋中白球的个数为3个;
(3)画树状图得:
∵共有16种等可能的结果,两次都摸到白球的有9种情况,
∴两次都摸到白球的概率为:$\frac{9}{16}$.
点评 此题考查了模拟实验以及频率求法和树状图法与列表法求概率,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

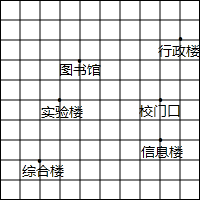 如图是某校的平面示意图,已知图书馆、校门口的坐标分别为(-2,2),(2,0),完成以下问题.
如图是某校的平面示意图,已知图书馆、校门口的坐标分别为(-2,2),(2,0),完成以下问题. 如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=20°,则∠AOB=80°.
如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=20°,则∠AOB=80°.