题目内容
19.计算:(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
分析 (1)原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及算术平方根定义计算即可得到结果;
(2)原式变形后,利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=1+3-4+2=2;
(2)原式=$\frac{{x}^{2}}{x-2}$-$\frac{4}{x-2}$=$\frac{{x}^{2}-4}{x-2}$=$\frac{(x+2)(x-2)}{x-2}$=x+2.
点评 此题考查了分式的加减法,以及实数的运算,分式加减法的关键是通分,通分的关键是找出最简公分母.

练习册系列答案
相关题目
9.若x=-2是关于x的方程(a-4)x-16=0的一个解,则a=( )
| A. | -4 | B. | 2 | C. | 4 | D. | 6 |
14.下列说法中正确的是( )
| A. | 不相交的两条直线叫做平行线 | |
| B. | 点到直线的距离是这点到直线的垂线段 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 在同一平面内,垂直于同一直线的两直线平行 |
9.若方程ax2-bx+8=x是关于x的一元一次方程,则a,b的值必须满足( )
| A. | a=0,b≠-1 | B. | a=0,b≠0 | C. | a≠0,b=-1 | D. | a≠0,b≠0 |

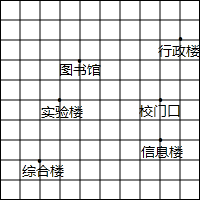 如图是某校的平面示意图,已知图书馆、校门口的坐标分别为(-2,2),(2,0),完成以下问题.
如图是某校的平面示意图,已知图书馆、校门口的坐标分别为(-2,2),(2,0),完成以下问题. 如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=20°,则∠AOB=80°.
如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=20°,则∠AOB=80°.