题目内容

10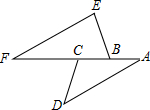．如图，已知点A、B、C、F在同一条直线上，AD∥EF，∠D=40°，∠F=30°，那么∠ACD的度数是110°．

分析 根据两直线平行，内错角相等可求∠A的度数，再根据三角形内角和定理即可得到∠ACD的度数，从而求解．

解答 解：∵AD∥EF，
∴∠A=∠F=30°，
∵∠D=40°，
∴∠ACD=180°-30°-40°=110°．
故答案为：110°．

点评 此题主要考查了平行线的性质及三角形内角和定理等知识点．本题的关键是求得∠A的度数．

练习册系列答案
相关题目
8．已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{mx+ny=8}\\{nx-my=1}\end{array}\right.$的解，则2m-n的算术平方根是（　　）
A．4B．2C．$\sqrt{2}$D．±2
2．（1）如图1，点M、N分别在∠AOB的边OA、OB上，且OM=ON，过点M、N分别作MP⊥OA、NP⊥OB，MP、NP交于P，E、F分别为线段MP、NP上的点，且∠EOF=$\frac{1}{2}$∠AOB，延长PM到S，使MS=NF，连接OS．则∠EOF与∠EOS的数量关系为相等，线段NF、EM、EF的数量关系为EF=NF+EM；
（2）如图2，点M、N分别在∠AOB的边OA、OB上，且OM=ON，∠OMP+∠ONP=180°，E、F分别为线段MP、NP上的点，且∠EOF=$\frac{1}{2}$∠AOB，（1）中的线段NF、EM、EF的数量关系是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．
（3）如图3，点M、N分别在∠AOB的边OA、OB上，且OM=ON，∠OMP+∠ONP=180°，E、F分别为线段PM、NP延长线上的点，且∠EOF=$\frac{1}{2}$∠AOB，（1）中线段NF、EM、EF的数量关系是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．
18．已知|a-3|+|b+1|=0，则a×b=-3．
5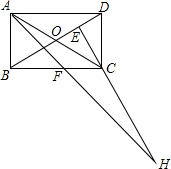．在矩形ABCD中，AB=1，AD=$\sqrt{3}$，AF平分∠DAB，过C点作CE⊥BD于E，延长AF、EC交于点H，下列结论中正确的是（　　）
①AF=$\frac{1}{2}$FH；②BO=BF；③CA=CH；④BE=3ED．
A．②③B．③④C．①②④D．②③④
15．计算：101×1022-101×982=（　　）
A．404B．808C．40400D．80800
2．如图，在△ABC中，∠ACB=90°，BC=AC=4，M为AB中点，D是射线BC上一动点，连接AD，将线段AD绕点A逆时针旋转90°得到线段AE，连接ED、ME，点D在运动过程中ME的最小值为（　　）
A．2B．2$\sqrt{2}$C．4D．4$\sqrt{2}$
19．若$\sqrt{x+3}$+|y-2|=0，则$\sqrt{x^y}$=（　　）
A．-3B．3C．±3D．$2\sqrt{2}$
19．已知a＜b，下列不等式中，变形正确的是（　　）
A．a-3＞b-3B．$\frac{a}{3}$＞$\frac{b}{3}$C．3a-1＞3b-1D．-3a＞-3b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网