题目内容
9.已知:分式$\frac{{x}^{2}+2x-3}{|x|-1}$的值为零,分式$\frac{{y}^{2}-3}{{y}^{2}+y-2}$无意义,则x+y的值是( )| A. | -5或-2 | B. | -1或-4 | C. | 1或4 | D. | 5或2 |
分析 分式的值为0的条件是:(1)分子为0;(2)分母不为0,可得x的值,根据分母为零分式无意义,可得y的值,再根据有理数的加法运算,可得答案.
解答 解:由分式$\frac{{x}^{2}+2x-3}{|x|-1}$的值为零,得
x2+2x-3=0且|x|-1≠0,
解得x=-3.
由分式$\frac{{y}^{2}-3}{{y}^{2}+y-2}$无意义,得
y2+y-2=0.
解得y=-2,y=1.
当x=-3,y=-2时,x+y=-5,
当x=-3,y=1时,x+y=-2,
故选:A.
点评 此题主要考查了分式值为零的条件,关键是掌握分式值为零的条件是分子等于零且分母不等于零.注意:“分母不为零”这个条件不能少.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.若关于x的方程2x-k+4=0的解是x=3,那么k的值是( )
| A. | 2 | B. | 10 | C. | -2 | D. | -10 |
17.已知a,d,c,b是成比例线段,其中a=3cm,b=2cm,c=6cm,则d的长度为( )
| A. | 4cm | B. | 1cm | C. | 9cm | D. | 5cm |
4.抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法错误的是( )
| A. | 抛物线开口向上 | B. | 抛物线的对称轴是x=1 | ||
| C. | 当x=1时,y的最大值为-4 | D. | c=-3 |
18.在实数-2,-3,0,1中,最小的实数是( )
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
19.若反比例函数y=$\frac{k}{x}$经过点(2,6),则此图象也经过下列点( )
| A. | (-2,6) | B. | (5,7) | C. | (4,3) | D. | (-6,2) |
 如图是用相同的小立方块搭成的一几何体,使得它从正面看和从上面看的形状如图所示,这样的几何体最少要8个立方块.
如图是用相同的小立方块搭成的一几何体,使得它从正面看和从上面看的形状如图所示,这样的几何体最少要8个立方块.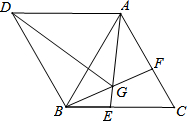 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.