题目内容
11.抛物线y=x2+2的图象与y轴的交点坐标是( )| A. | (-2,0) | B. | (2,0) | C. | (0,-2) | D. | (0,2) |
分析 根据y轴上点的坐标特征,计算自变量为0时的函数值即可.
解答 解:当x=0时,y=x2+2=2,
所以抛物线y=x2+2的图象与y轴的交点坐标是(0,2).
故选D.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式,即已知横坐标可求对应的纵坐标.本题的关键是确定y轴上点的坐标特征.

练习册系列答案
相关题目
19.若反比例函数y=$\frac{k}{x}$经过点(2,6),则此图象也经过下列点( )
| A. | (-2,6) | B. | (5,7) | C. | (4,3) | D. | (-6,2) |
6. 长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
 长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
3.已知点(-1,y1),(-2,y2),(2,y3)在函数y=2(x-1)2的图象上,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y2>y3>y1 | D. | y3>y1>y2 |
20.世界上有一种最薄的金箔,其厚度约为0.000000092m,将0.000000092用科学记数法表示为( )
| A. | 0.92×10-7 | B. | 9.2×10-8 | C. | 9.2×10-7 | D. | 0.92×10-8 |
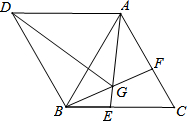 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
 在?ABCD中,M是AB延长线上一点,E是BC的中点,连接ME并延长,交CD于F,交AD延长线于点N,若$\frac{BM}{CD}=\frac{2}{5}$,BC=4,则AN=7.
在?ABCD中,M是AB延长线上一点,E是BC的中点,连接ME并延长,交CD于F,交AD延长线于点N,若$\frac{BM}{CD}=\frac{2}{5}$,BC=4,则AN=7.