题目内容
10. (1)请仔细观察并根据下列函数图,结合生活实际,编一个故事,使故事情境中出现的一对变量x,y满足图示的函数关系式,要求:
(1)请仔细观察并根据下列函数图,结合生活实际,编一个故事,使故事情境中出现的一对变量x,y满足图示的函数关系式,要求:①指出x和y的含义;
②利用图中数据说明这对变量变化过程的实际意义;
(2)结合编写的故事情节及函数图象解释点C的实际意义并求出点C的坐标.
分析 (1)利用行程问题结合图象编写故事即可;
(2)设出线段BC表示的函数解析式,利用待定系数法求函数解析式,进一步得出点C坐标即可.
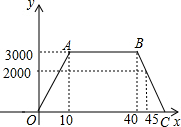
解答 解:(1)故事:小明骑自行车去植物园,从家出发,走了10分钟到达距离家3000米的植物园游玩,游玩了30分钟后,提高了速度回家.
①x表示时间,y表示距离家的路程;
②小明以300m/min的速度匀速骑了10min到达植物园,在植物园游玩了30min,然后以400m/min的速度匀速骑车回到家.
(2)设线段BC表示的函数解析式为y=kx+b,代入(40,3000),(45,2000)得
$\left\{\begin{array}{l}{40k+b=3000}\\{45k+b=2000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-200}\\{b=11000}\end{array}\right.$.
故线段BC表示函数解析式为y=-200x+11000,
令y=0,则-200x+11000=0,
解得:x=55.
点C的坐标为(55,0),表示小明从开始出发到回家总共用时55分钟.
点评 此题考查一次函数的实际运用,看清图意,结合实际,利用待定系数法求函数解析式解决问题.

练习册系列答案
相关题目
20.若关于x的方程2x-k+4=0的解是x=3,那么k的值是( )
| A. | 2 | B. | 10 | C. | -2 | D. | -10 |
18.在实数-2,-3,0,1中,最小的实数是( )
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
5.计算(-2)2015+3×(-2)2014的结果是( )
| A. | -22014 | B. | 22014 | C. | 1 | D. | -22015 |
19.若反比例函数y=$\frac{k}{x}$经过点(2,6),则此图象也经过下列点( )
| A. | (-2,6) | B. | (5,7) | C. | (4,3) | D. | (-6,2) |
20.世界上有一种最薄的金箔,其厚度约为0.000000092m,将0.000000092用科学记数法表示为( )
| A. | 0.92×10-7 | B. | 9.2×10-8 | C. | 9.2×10-7 | D. | 0.92×10-8 |
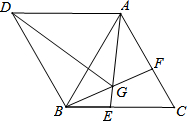 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.