题目内容
11. 如图,?ABCD中,EF∥AB,DE:EA=1:2,EF=4,则CD的长为( )
如图,?ABCD中,EF∥AB,DE:EA=1:2,EF=4,则CD的长为( )| A. | $\frac{4}{3}$ | B. | 8 | C. | 12 | D. | 16 |
分析 由EF∥AB,DE:EA=1:2,根据平行线分线段成比例定理,可得EF:AB=1:3,继而求得AB的长,然后由平行四边形的性质,求得答案.
解答 解:∵DE:EA=1:2,
∴DE:DA=1:3,
∵EF∥AB,
∴EF:AB=DE:DA=1:3,
∵EF=4,
∴AB=12,
∵四边形ABCD是平行四边形,
∴CD=AB=12.
故选C.
点评 此题考查了平行线分线段成比例定理以及平行四边形的性质.注意掌握线段的对应关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.多项式1-4t+4t2可以分解为( )
| A. | (4t-1)2 | B. | -(2t-1)2 | C. | (2t-1)2 | D. | (1-4t)2 |
16.下列各式中,正确的是( )
| A. | $\frac{a+b}{ab}$=$\frac{1+b}{b}$ | B. | $\frac{x-y}{x+y}$=$\frac{{x}^{2}-{y}^{2}}{(x+y)^{2}}$ | ||
| C. | $\frac{x-3}{{x}^{2}-9}$=$\frac{1}{x-3}$ | D. | $\frac{-x+y}{2}$=-$\frac{x+y}{2}$ |
20.若关于x的方程2x-k+4=0的解是x=3,那么k的值是( )
| A. | 2 | B. | 10 | C. | -2 | D. | -10 |
 如图是用相同的小立方块搭成的一几何体,使得它从正面看和从上面看的形状如图所示,这样的几何体最少要8个立方块.
如图是用相同的小立方块搭成的一几何体,使得它从正面看和从上面看的形状如图所示,这样的几何体最少要8个立方块.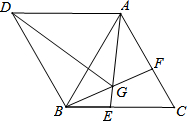 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.