题目内容
3.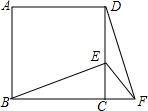 如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.(1)△DCF可以看做是△BCE绕点C旋转某个角度得到的吗?说明理由.
(2)若∠CEB=60°,求∠EFD的度数.
分析 (1)根据正方形的性质及全等三角形的判定方法即可证明△BCE≌△DCF,据此即可解答;
(2)由两个三角形全等的性质得出∠CFD的度数,再用等腰三角形的性质求∠EFD的度数.
解答 (1)证明:∵四边形ABCD是正方形,
∴DC=BC,∠DCB=∠FCE,
∵CE=CF,
∴△DCF≌△BCE,
则△DCF可以看作是△BCE绕点C顺时针旋转90°得到;
(2)解:∵△BCE≌△DCF,
∴∠DFC=∠BEC=60°,
∵CE=CF,
∴∠CFE=45°,
∴∠EFD=15°.
点评 此题主要考查正方形的特殊性质及全等三角形的判定的综合运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
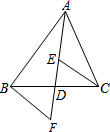 AD是△ABC的中线,DE=DF.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
AD是△ABC的中线,DE=DF.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )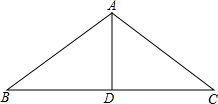 如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:BD=CD.
如图,已知△ABC中,AB=AC,AD平分∠BAC,求证:BD=CD.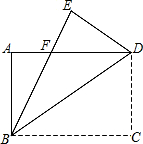 如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?
如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?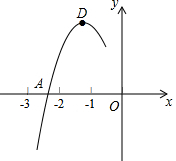 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c<0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.其中正确的结论有②③④(填序号).
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c<0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.其中正确的结论有②③④(填序号). 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.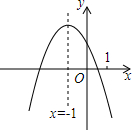 二次函数 y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④abc>0,其中正确结论是①③④.(填序号)
二次函数 y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④abc>0,其中正确结论是①③④.(填序号)