题目内容
15．点A、B、C在同一条直线上，AB=6，BC=10，D、E分别是AB、BC的中点，DE的长8或2．分析 根据中点定义求出BD、BE的长度，然后分①点C在AB的延长线上时，求出DE的长度；②点C在AB的反向延长线上时，求出DE的长度．
解答 
解：∵D、E分别是线段AB、BC的中点，AB=12cm，BC=4cm，
∴BD=$\frac{1}{2}$AB=3，BE=$\frac{1}{2}$BC=5，
①如图1，点C在AB的延长线上时，DE=BD+BE=3+5=8，
②如图2，点C在AB的反向延长线上时，DE=BE-BD=5-3=2，
故答案为：8或2．
点评 本题考查了两点间的距离，线段中点的定义，难点在于要分情况讨论，作出图形更形象直观．
练习册系列答案
考前必练系列答案
相关题目
3．
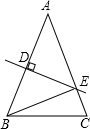已知：如图，在△ABC中，AB=AC，DE是AB的垂直平分线，若BE+CE=12，BC=8，则△ABC的周长为（ ）
已知：如图，在△ABC中，AB=AC，DE是AB的垂直平分线，若BE+CE=12，BC=8，则△ABC的周长为（ ）| A． | 20 | B． | 32 | C． | 24 | D． | 36 |
10．四边形ABCD是正方形，以CD为边向正方形外作正△CDE，则∠EAB的度数为（ ）
| A． | 75° | B． | 72° | C． | 67.5° | D． | 65° |
7．
如图所示，四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH…，如此下去，则第2017个正方形的边长是（ ）
如图所示，四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH…，如此下去，则第2017个正方形的边长是（ ）| A． | ${（{\sqrt{2}}）^{2016}}$ | B． | ${（{\sqrt{2}}）^{2017}}$ | C． | $2016\sqrt{2}$ | D． | $2017\sqrt{2}$ |