题目内容
7. 如图所示,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH…,如此下去,则第2017个正方形的边长是( )
如图所示,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH…,如此下去,则第2017个正方形的边长是( )| A. | ${({\sqrt{2}})^{2016}}$ | B. | ${({\sqrt{2}})^{2017}}$ | C. | $2016\sqrt{2}$ | D. | $2017\sqrt{2}$ |
分析 根据正方形的对角线等于边长的$\sqrt{2}$倍依次求解,然后根据指数的变化求出第n个正方形的边长即可.
解答 解:∵四边形ABCD是边长为1的正方形,
∴第二个正方形ACEF的边长AC=$\sqrt{2}$,
第三个正方形AEGH的边长AE=$\sqrt{2}$AC=($\sqrt{2}$)2,
…,
第n个正方形的边长=($\sqrt{2}$)n-1.
∴第2017个正方形的边长是($\sqrt{2}$)2016,
故选A.
点评 本题考查了正方形的性质,主要利用了正方形的对角线等于边长的$\sqrt{2}$倍的性质,注意正方形的序数与指数的关系是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F.若S△DEF=3,则S?ABCD=36.
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F.若S△DEF=3,则S?ABCD=36.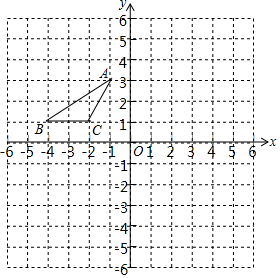 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图. 如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.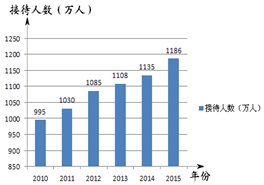 从世妇会NGO论坛到APEC会议、“一带一路”国际峰会,怀柔区正向着积极打造“国际会都”的目标迈进,也吸引着海内外游客到怀柔观光旅游.如图为2010年到2015年我区年接待旅游人数的统计图.
从世妇会NGO论坛到APEC会议、“一带一路”国际峰会,怀柔区正向着积极打造“国际会都”的目标迈进,也吸引着海内外游客到怀柔观光旅游.如图为2010年到2015年我区年接待旅游人数的统计图.