题目内容
6.函数y=kx+b的图象与函数y=-$\frac{1}{2}$x+3的图象平行,且与y轴的交点为M(0,-2),则其函数表达式为y=-$\frac{1}{2}$x-2.分析 先根据所求函数的图象与已知函数的图象平行得出所求函数的斜率,然后把已知点代入函数解析式,即可求出各个系数,从而利用待定系数法求出函数的表达式.
解答 解:∵函数y=kx+b的图象与函数y=-$\frac{1}{2}$+3的图象平行
∴k=-$\frac{1}{2}$
∵y=kx+b与y轴的交点为M(0,-2)
∴b=-2
将k=-$\frac{1}{2}$,b=2代入y=kx+b可得y=-$\frac{1}{2}$x-2
故答案为:y=-$\frac{1}{2}$x-2.
点评 本题考查了两直线平行的问题,根据平行直线的解析式的k值相等求出k的值是解题的关键,也是本题的难点.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
1. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,以半圆的半径8为直径在半圆内作一个圆,求图中阴影部分的面积.
如图,以半圆的半径8为直径在半圆内作一个圆,求图中阴影部分的面积.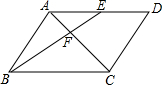 如图所示,平行四边形ABCD中,点E是AD边的中点,BE交对角线AC于点F.若AF=2,则对角线AC的长为( )
如图所示,平行四边形ABCD中,点E是AD边的中点,BE交对角线AC于点F.若AF=2,则对角线AC的长为( ) 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F.若S△DEF=3,则S?ABCD=36.
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F.若S△DEF=3,则S?ABCD=36.