题目内容
5．
如图，在Rt△ABC中，∠ACB=90°，∠B=2∠A，CD是△ABC的中线，求证：△BCD是等边三角形．
分析 根据三角形的内角和得到∠B=60°，由直角三角形的性质，斜边上的中线等于斜边的一半，进而得出△CDB是等边三角形．
解答 解：∵∠ACB=90°，∠B=2∠A，
∴∠B=60°，
∵CD是△ABC的中线，
∴CD=$\frac{1}{2}$AB=BD，
∴△BCD是等边三角形．
点评 此题主要考查了等边三角形的判定，得出CD=BD是解题关键．
练习册系列答案
相关题目
如图，AB是⊙O的弦，半径OD⊥AB于E，AB=24cm，AD=13cm，则OD=$\frac{169}{10}$cm．
13．
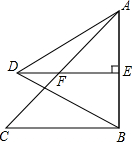如图，△ABC是等腰直角三角形，∠ABC=90°，AB=10，以AB为边向左边作一个等边△ABD，过点D作DE⊥AB于点E，交AC于点F．
（1）求证：△AEF是等腰直角三角形；
（2）求DF的长．
如图，△ABC是等腰直角三角形，∠ABC=90°，AB=10，以AB为边向左边作一个等边△ABD，过点D作DE⊥AB于点E，交AC于点F．（1）求证：△AEF是等腰直角三角形；
（2）求DF的长．
10．判定△ABC∽△A′B′C′，已知∠C′=∠C=90°，则应有哪个条件（ ）
| A． | ∠B=∠B′ | B． | $\frac{A′B′}{AB}$=$\frac{A′C′}{AC}$ | C． | $\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$ | D． | 以上说法都对 |
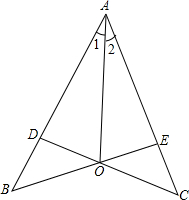如图，已知∠BEC=∠BDC，BE=CD，求证：∠1=∠2．