题目内容
13．
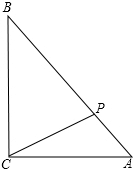如图所示，在R△ABC中，∠C=90°，AC=6，AB=10，点P为AB上一点，设PB=x，△ACP的面积为y，写出y与x之间的函数关系式及x的取值范围．
分析 根据三角形的面积，可得C到AB的距离，再根据三角形的面积公式，可得答案．
解答 解：由勾股定理，得
BC=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
由三角形的面积，得
C到AB的距离$\frac{6×8}{10}$=$\frac{24}{5}$．
y与x之间的函数关系式y=$\frac{1}{2}$（10-x）×$\frac{24}{5}$，
10-x＞0，解得x＜10，
x的取值范围0≤x＜10．
点评 本题考查了函数关系式，利用三角形的面积得出C到AB的距离是解题关键．
练习册系列答案
相关题目
如图，在锐角三角形ABC中，sinB=$\frac{3}{5}$，tanC=3，且S△ABC=20，求BC的长．