题目内容
8.化简下列各式:(1)$\sqrt{12}$$+\frac{1}{3}\sqrt{27}$;
(2)$\frac{\sqrt{20}+\sqrt{5}}{\sqrt{5}}$-4;
(3)$\sqrt{125}$$-2\sqrt{45}$$-\sqrt{\frac{1}{5}}$;
(4)$\sqrt{32}$$-3\sqrt{\frac{1}{2}}$+$\sqrt{2}$;
(5)$\sqrt{0.6}$$+\sqrt{1\frac{2}{3}}$;
(6)(2$\sqrt{2}$+3)×(2$\sqrt{2}$-3);
(7)(3$\sqrt{2}-\sqrt{7}$)2;
(8)$\sqrt{1{0}^{2}-{8}^{2}}$+($\sqrt{10}$)2+|2-$\sqrt{5}$|;
(9)$\frac{\sqrt{18}×\sqrt{6}}{\sqrt{3}}$.
分析 根据二次根式的运算性质即可求出答案.
解答 解:(1)原式=2$\sqrt{3}$+$\frac{1}{3}$×3$\sqrt{3}$=3$\sqrt{3}$;
(2)原式=$\frac{2\sqrt{5}+\sqrt{5}}{\sqrt{5}}$-4=3-4=-1;
(3)原式=5$\sqrt{5}$-6$\sqrt{5}$-$\frac{\sqrt{5}}{5}$=-$\frac{6}{5}$$\sqrt{5}$;
(4)原式=4$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$+$\sqrt{2}$=$\frac{7}{2}$$\sqrt{2}$;
(5)原式=$\frac{\sqrt{15}}{5}$-$\frac{\sqrt{15}}{3}$=-$\frac{2\sqrt{15}}{15}$;
(6)原式=4×2-9=-1;
(7)原式=(3$\sqrt{2}$)2-2×3$\sqrt{2}$×$\sqrt{7}$+($\sqrt{7}$)2=25-6$\sqrt{14}$;
(8)原式=$\sqrt{36}$+10+$\sqrt{5}$-2=6+10+$\sqrt{5}$-2=14+$\sqrt{5}$;
(9)原式=$\frac{3\sqrt{2}×\sqrt{6}}{\sqrt{3}}$=3×2=6.
点评 本题考查二次根式的混合运算,涉及二次根式的运算性质,属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列各分式中,最简分式是( )
| A. | $\frac{12(x-y)}{15(x+y)}$ | B. | $\frac{{y}^{2}-{x}^{2}}{x+y}$ | ||
| C. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}y+x{y}^{2}}$ | D. | $\frac{{x}^{2}-{y}^{2}}{(x+y)^{2}}$ |
17.五箱苹果的质量分别为(单位:千克):18,20,21,22,19.则这五箱苹果质量的中位数为( )
| A. | 20 | B. | 19 | C. | 20 | D. | 21 |
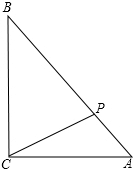 如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.
如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.