题目内容
5.已知一次函数y=kx+b的图象与x轴交于点A(-6,0),与y轴交于点B,若△AOB的面积为12,且y随x增大而减小,求一次函数的解析式.分析 首先根据图象经过点A(-6,0),可得0=-6k+b,进而得到b=6k,再根据△AOB的面积为12可得:$\frac{1}{2}$AO•OB=12,进而可得$\frac{1}{2}$•6•|b|=12,算出|b|的值,再计算出b,然后把b的值代入b=6k即可算出答案.
解答 解:∵图象经过点A(-6,0),
∴0=-6k+b,
即b=6k ①,
∵图象与y轴的交点是B(0,b),
∴$\frac{1}{2}$AO•OB=12,
即:$\frac{1}{2}$•6•|b|=12,
∴|b|=4,
∴b1=4,b2=-4,
代入①式,得k1=$\frac{2}{3}$,k2=-$\frac{2}{3}$,
一次函数的表达式是y=$\frac{2}{3}$x+4或y=-$\frac{2}{3}$x-4.
点评 此题主要考查了求一次函数解析式,关键计算出|b|的值,注意b有两个值,不要片面的得到一个值.

练习册系列答案
相关题目
17.五箱苹果的质量分别为(单位:千克):18,20,21,22,19.则这五箱苹果质量的中位数为( )
| A. | 20 | B. | 19 | C. | 20 | D. | 21 |
 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=75°,∠C=45°,求∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=75°,∠C=45°,求∠DAE的度数.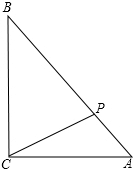 如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.
如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围. 如图,CD所在的直线垂直平分线段AB,怎样用这样的“T”形工具找到圆形工件的圆心?
如图,CD所在的直线垂直平分线段AB,怎样用这样的“T”形工具找到圆形工件的圆心?