题目内容
3. 如图,在锐角三角形ABC中,sinB=$\frac{3}{5}$,tanC=3,且S△ABC=20,求BC的长.
如图,在锐角三角形ABC中,sinB=$\frac{3}{5}$,tanC=3,且S△ABC=20,求BC的长.
分析 根据题意先作出边BC上的高AD,然后根据sinB=$\frac{3}{5}$,tanC=3,且S△ABC=20,可以求得BC的长,本题得以解决.
解答 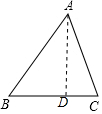 解:作AD⊥BC于点D,如右图所示,
解:作AD⊥BC于点D,如右图所示,
∵sinB=$\frac{AD}{AB}$=$\frac{3}{5}$,tanC=$\frac{AD}{CD}$=3,
∴设AD=3a,则AB=5a,CD=a,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}=\sqrt{(5a)^{2}-(3a)^{2}}$=4a,
∴BC=BD+DC=4a+a=5a,
∵S△ABC=20,
∴$\frac{5a•3a}{2}$=20,
解得,a=$\sqrt{5}$或a=-$\sqrt{5}$(舍去),
∴5a=5$\sqrt{5}$,
即BC的长是5$\sqrt{5}$.
点评 本题考查解直角三角形,解题的关键是明确题意,画出相应的图形,利用锐角三角函数解答.

练习册系列答案
相关题目
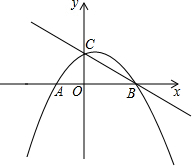 如图.在平面直角坐标系中.抛物线y=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+2与x轴交于A、B两点,与y轴交于点C,点P从B出发.沿射线BA方向以每秒1个单位的速度匀速运动.过点P作PQ⊥x轴.直线PQ分别与直线BC、抛物线交于点Q、K.
如图.在平面直角坐标系中.抛物线y=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+2与x轴交于A、B两点,与y轴交于点C,点P从B出发.沿射线BA方向以每秒1个单位的速度匀速运动.过点P作PQ⊥x轴.直线PQ分别与直线BC、抛物线交于点Q、K. 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=75°,∠C=45°,求∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=75°,∠C=45°,求∠DAE的度数.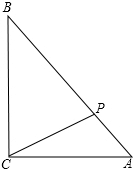 如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.
如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.