题目内容
11. 如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为10cm,小圆半径为6cm,则弦AB的长为16cm.
如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为10cm,小圆半径为6cm,则弦AB的长为16cm.
分析 连结OC,OA,如图,先根据切线的性质得OC⊥AB,再根据垂径定理得到AC=BC,然后利用勾股定理计算出AC,从而可得到AB的长.
解答 解:连结OC,OA,如图,
∵大圆的弦AB与小圆相切于点C,
∴OC⊥AB,
∴∠ACO=90°,AC=BC,
在Rt△AOC中,AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴AB=2AC=16(cm).
故答案为16cm.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
2.计算:
(1)$\sqrt{{6}^{2}}$;(2)$\sqrt{(-5)^{2}}$;
(3)$\sqrt{(a+1)^{2}}$(a≥-1);(4)$\sqrt{(x-2)^{2}}$(x≤2)
(1)$\sqrt{{6}^{2}}$;(2)$\sqrt{(-5)^{2}}$;
(3)$\sqrt{(a+1)^{2}}$(a≥-1);(4)$\sqrt{(x-2)^{2}}$(x≤2)
16.下列调查中,适宜采用全面调查(普查)方式的是( )
| A. | 调查长江流域的水污染情况 | |
| B. | 调查重庆市民对中央电视台2016年春节联欢晚会的满意度 | |
| C. | 为保证我国首艘航母“瓦良格”的成功试航,对其零部件进行检查 | |
| D. | 调查一批新型节能灯泡的使用寿命 |
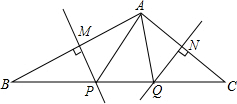 如图,在△ABC的边AB和AC的垂直平分线分别交BC于P、Q,若∠BAC=100°,则∠PAQ=20;若∠BAC+∠PAQ=150°,则∠PAQ=40°.
如图,在△ABC的边AB和AC的垂直平分线分别交BC于P、Q,若∠BAC=100°,则∠PAQ=20;若∠BAC+∠PAQ=150°,则∠PAQ=40°.