题目内容
3.已知(1,y1),($\frac{1}{2}$,y2)两点都在一次函数y=$\frac{1}{2}$x-3的图象上,则y1>y2(填“>”“<”或“﹦”)分析 直接把(1,y1),($\frac{1}{2}$,y2)代入一次函数y=$\frac{1}{2}$x-3,可得y1、y2的值,进而可得答案.
解答 解:∵(1,y1),($\frac{1}{2}$,y2)两点都在一次函数y=$\frac{1}{2}$x-3的图象上,
∴y1=$\frac{1}{2}×1$-3=-$\frac{5}{2}$,y2=$\frac{1}{2}×\frac{1}{2}$-3=-$\frac{11}{4}$,
∴y1>y2,
故答案为:>.
点评 此题主要考查了一次函数图象上点的坐标特点,关键是掌握凡是函数图象经过的点必能满足解析式.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
14.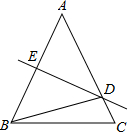 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )| A. | 50° | B. | 20° | C. | 30° | D. | 25° |
15.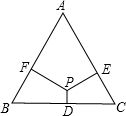 如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
 如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )| A. | 10 | B. | 15 | C. | $\frac{40}{3}$ | D. | $\frac{50}{3}$ |
 如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为10cm,小圆半径为6cm,则弦AB的长为16cm.
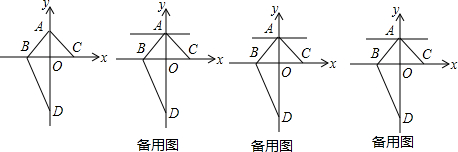
如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为10cm,小圆半径为6cm,则弦AB的长为16cm. 已知边长为2的正方形OABC在直角坐标系中(如图),OA与y轴的夹角为30°,求点A、点C、点B的坐标.
已知边长为2的正方形OABC在直角坐标系中(如图),OA与y轴的夹角为30°,求点A、点C、点B的坐标.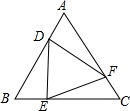 如图,等边△ABC中,点D、E、F分别同时从点A、B、C出发,以相同的速度在AB、BC、CA上运动,连结DE、EF、DF.
如图,等边△ABC中,点D、E、F分别同时从点A、B、C出发,以相同的速度在AB、BC、CA上运动,连结DE、EF、DF.