题目内容
20.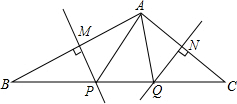 如图,在△ABC的边AB和AC的垂直平分线分别交BC于P、Q,若∠BAC=100°,则∠PAQ=20;若∠BAC+∠PAQ=150°,则∠PAQ=40°.
如图,在△ABC的边AB和AC的垂直平分线分别交BC于P、Q,若∠BAC=100°,则∠PAQ=20;若∠BAC+∠PAQ=150°,则∠PAQ=40°.
分析 根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AP=BP,AQ=CQ,再根据三角形内角和定理求出∠B+∠C,再根据等边对等角的性质可得∠BAP=∠B,∠CAQ=∠C,然后代入数据进行计算即可得解.根据∠BAC+∠PAQ=150°,可得∠1+∠2+2∠PAQ=150°①,再由三角形内角和为180°可得∠B+∠C+∠1+∠2+∠PAQ=180°②,然后②-①得③,再①-③可得答案.
解答 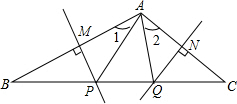 解:∵MP、NQ分别是AB、AC的垂直平分线,
解:∵MP、NQ分别是AB、AC的垂直平分线,
∴AP=BP,AQ=CQ,
∴∠1=∠B,∠2=∠C,
∵∠BAC=100°,
∴∠B+∠C=180°-100°=80°,
∴∠1+∠2=80°,
∴∠PAQ=100°-80°=20°;
∵∠BAC+∠PAQ=150°,
∴∠1+∠2+2∠PAQ=150°,①
∵∠B+∠C+∠1+∠2+∠PAQ=180°,②
∴②-①得:
∠B+∠C-∠PAQ=30°,③
∵∠1=∠B,∠2=∠C,
∴①-③得:∠PAQ=40°,
故答案为:40°.
点评 此题主要考查了线段垂直平分线的性质,关键是掌握线段垂直平分线上的点到线段两端点的距离相等.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
15.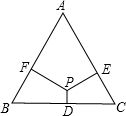 如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
 如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )
如图,P为等腰三角形ABC内一点,过P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F.已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3.则四边形PDCE的面积为( )| A. | 10 | B. | 15 | C. | $\frac{40}{3}$ | D. | $\frac{50}{3}$ |
5.若m等于它的倒数,则分式$\frac{{m}^{2}-4m+4}{{m}^{2}-4}÷(m-2)$的值为( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{1}{3}$或1 | D. | 以上都不对 |
9. 如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )
如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )
 如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )
如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
10.(-$\frac{1}{3}$)-1-4cos30°+|-$\sqrt{12}$|的计算结果为( )
| A. | -4 | B. | 4 | C. | -3 | D. | -2 |




 如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为10cm,小圆半径为6cm,则弦AB的长为16cm.
如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为10cm,小圆半径为6cm,则弦AB的长为16cm. 已知边长为2的正方形OABC在直角坐标系中(如图),OA与y轴的夹角为30°,求点A、点C、点B的坐标.
已知边长为2的正方形OABC在直角坐标系中(如图),OA与y轴的夹角为30°,求点A、点C、点B的坐标.