题目内容
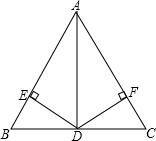 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF,∠BAD=18°,求:∠CAD的度数.
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF,∠BAD=18°,求:∠CAD的度数.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:先根据HL证明Rt△BDE≌Rt△CDF,得出DE=DF,再根据角平分线的判定定理,证出AD平分∠BAC,即可得出结果.
解答:
解:∵D是BC的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
∴AD平分∠BAC,
∴∠CAD=∠BAD=18°.
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在Rt△BDE和Rt△CDF中,
|
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
∴AD平分∠BAC,
∴∠CAD=∠BAD=18°.
点评:本题考查了全等三角形的判定与性质以及角平分线的判定定理;证明三角形全等得出DE=DF是解决问题的关键.

练习册系列答案
相关题目
 如图所示,△ABC中,AB=BC=AC,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图所示,△ABC中,AB=BC=AC,BD=CE,AD与BE相交于点P,则∠APE的度数是( )| A、45° | B、55° |
| C、75° | D、60° |
用直接开平方法解方程(x+m)2=n,下列结论正确的是( )
A、有两个根,为x=±
| ||
B、当n>0时,有两个根,为x=±
| ||
C、当x>0时,有两个根,为x=±
| ||
| D、当n<0时,无实数根 |
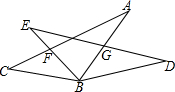 如图,BC=BE,∠C=∠E,∠CBE=∠ABD,则下列结论错误的是( )
如图,BC=BE,∠C=∠E,∠CBE=∠ABD,则下列结论错误的是( )| A、∠A=∠D |
| B、BF=BG |
| C、AC=DE |
| D、BA=BD |
 如图,已知△ABC中,DE∥BC,将△ADE沿DE翻折,点A落在平面内的A′处,若∠BDA′=70°,则∠B的度数是
如图,已知△ABC中,DE∥BC,将△ADE沿DE翻折,点A落在平面内的A′处,若∠BDA′=70°,则∠B的度数是
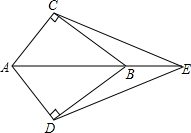 如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD 某班在一次测试中,一道计算题(满分5分)的得分情况如图.则这题得分的平均数是
某班在一次测试中,一道计算题(满分5分)的得分情况如图.则这题得分的平均数是