题目内容
在平面直角坐标系中,抛物线C1:y=ax2+4x+4a (0<a<2),
(1)当C1与x轴有唯一交点时,求C1的解析式.
(2)若a=1,将抛物线C1先向右平移2个单位,再向下平移1个单位得抛物线C2,抛物线C2与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C2相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍.求k的值.
(3)若A(1,yA),B(0,yB),C(-1,yc)三点均在C1上,连BC,作AE∥BC交抛物线C1于E,求证:当a值变化时,E点在一条直线上.
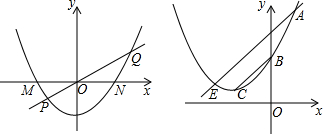
(1)当C1与x轴有唯一交点时,求C1的解析式.
(2)若a=1,将抛物线C1先向右平移2个单位,再向下平移1个单位得抛物线C2,抛物线C2与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C2相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍.求k的值.
(3)若A(1,yA),B(0,yB),C(-1,yc)三点均在C1上,连BC,作AE∥BC交抛物线C1于E,求证:当a值变化时,E点在一条直线上.
考点:二次函数综合题
专题:压轴题
分析:(1)利用根的判别式列方程求出a,然后写出即可;
(2)先求出平移后的抛物线的解析式,再设点P(x,y),Q(xQ,yQ),根据三角形的面积求出yQ=4y,从而得到xQ=-4x,然后根据点P、Q是抛物线与直线的交点,利用根与系数的关系求出点P、Q的横坐标,再求出k值即可;
(3)作CD⊥y轴于D,作AQ⊥x轴于Q,作EG⊥AQ于G,求出△AEG与△BCD相似,设E(x,y),然后表示出AG、EG、BD、CD,再根据相似三角形对应边成比例列式求解得到x=-2.
(2)先求出平移后的抛物线的解析式,再设点P(x,y),Q(xQ,yQ),根据三角形的面积求出yQ=4y,从而得到xQ=-4x,然后根据点P、Q是抛物线与直线的交点,利用根与系数的关系求出点P、Q的横坐标,再求出k值即可;
(3)作CD⊥y轴于D,作AQ⊥x轴于Q,作EG⊥AQ于G,求出△AEG与△BCD相似,设E(x,y),然后表示出AG、EG、BD、CD,再根据相似三角形对应边成比例列式求解得到x=-2.
解答:
解:(1)∵C1与x轴有唯一交点,
∴△=42-4•a•a=0,
解得a=±1,
∵0<a<2,
∴a=1,
∴C1的解析式为y=x2+4x+4;
(2)y=x2+4x+4=(x+2)2,
∵抛物线C1先向右平移2个单位,再向下平移1个单位得抛物线C2,
∴抛物线C2为y=x2-1,
∴MO=NO,
设P(x,y),Q(xQ,yQ),
∵△NOQ的面积是△MOP的面积的4倍,
∴yQ=-4y,
∴xQ=-4x,
∵x、xQ为方程x2-1=kx的两根,
∴x•xQ=-1,
∴x=-
,xQ=2,
∴k=(-
+2)=
;
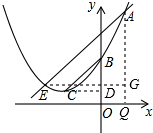
(3)作CD⊥y轴于D,作AQ⊥x轴于Q,作EG⊥AQ于G,
则△AEG∽△BCD,
∴
=
,
设E(x,y),
∴yA=a+4+4a=5a+4,yB=4a,yC=a-4+4a=5a-4,yE=ax2+4x+4a,
∴AG=(5a+4)-(ax2+4x+4a)=a(1-x2)+4(1-x),
EG=1-x,
BD=4a-(5a-4)=4-a,
CD=1,
所以,
=
,
∵x≠1,
∴a(1+x)+4=4-a,
解得x=-2,
即:E点在直线x=-2上.
∴△=42-4•a•a=0,
解得a=±1,
∵0<a<2,
∴a=1,
∴C1的解析式为y=x2+4x+4;
(2)y=x2+4x+4=(x+2)2,
∵抛物线C1先向右平移2个单位,再向下平移1个单位得抛物线C2,
∴抛物线C2为y=x2-1,
∴MO=NO,
设P(x,y),Q(xQ,yQ),
∵△NOQ的面积是△MOP的面积的4倍,
∴yQ=-4y,
∴xQ=-4x,
∵x、xQ为方程x2-1=kx的两根,
∴x•xQ=-1,
∴x=-
| 1 |
| 2 |
∴k=(-
| 1 |
| 2 |
| 3 |
| 2 |

(3)作CD⊥y轴于D,作AQ⊥x轴于Q,作EG⊥AQ于G,
则△AEG∽△BCD,
∴
| AG |
| BD |
| EG |
| CD |
设E(x,y),
∴yA=a+4+4a=5a+4,yB=4a,yC=a-4+4a=5a-4,yE=ax2+4x+4a,
∴AG=(5a+4)-(ax2+4x+4a)=a(1-x2)+4(1-x),
EG=1-x,
BD=4a-(5a-4)=4-a,
CD=1,
所以,
| a(1-x2)+4(1-x) |
| 4-a |
| 1-x |
| 1 |
∵x≠1,
∴a(1+x)+4=4-a,
解得x=-2,
即:E点在直线x=-2上.
点评:本题是二次函数综合题型,主要利用了抛物线与x轴的交点问题,根的判别式,二次函数图象与几何变换,三角形的面积,相似三角形的面积,难点在于(3)作辅助线构造出相似三角形.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
已知a2+3ab+b2=0(a≠0,b≠0),则代数式
+
的值等于( )
| b |
| a |
| a |
| b |
| A、3 | ||
| B、-3 | ||
C、
| ||
| D、无法确定 |
在
,-
,
,π,这四个数中,无理数有( )
| 22 |
| 7 |
| 3 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
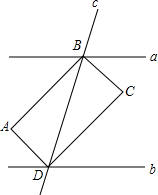 如图,已知a∥b,a不垂直于c,BA,DA,DC,BC分别是同旁内角角平分线,则与∠ABC相等的角有( )个.
如图,已知a∥b,a不垂直于c,BA,DA,DC,BC分别是同旁内角角平分线,则与∠ABC相等的角有( )个.
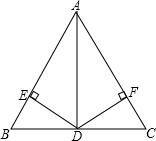 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF,∠BAD=18°,求:∠CAD的度数.
如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF,∠BAD=18°,求:∠CAD的度数.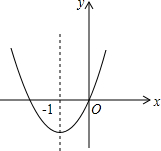 二次函数y=x2+bx的图象如图,对称轴为x=-1,若关于x的一元二次方程x2+bx-t=0(t为实数)在-4<x<1的范围内有解,则t的取值范围是
二次函数y=x2+bx的图象如图,对称轴为x=-1,若关于x的一元二次方程x2+bx-t=0(t为实数)在-4<x<1的范围内有解,则t的取值范围是