题目内容
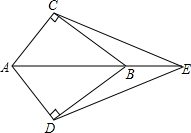如图所示，E为AB延长线上的一点，AC⊥BC，AD⊥BD，AC=AD求证：∠CEA=∠DEA．
考点：全等三角形的判定与性质
专题：证明题
分析：首先利用“HL”证明Rt△ABC≌Rt△ABD，得出∠CAB=∠DAB，进一步利用“SAS”证得△ACE≌△ADE，证得∠CEA=∠DEA．
解答：
证明：∵AC⊥BC，AD⊥BD，
∴∠ACB=∠ADB=90°，
在Rt△ABC和Rt△ABD中，
∴Rt△ABC≌Rt△ABD（HL），
∴∠CAB=∠DAB，
在△ACE和△ADE中，
∴△ACE≌△ADE，
∴∠CEA=∠DEA．
∴∠ACB=∠ADB=90°，
在Rt△ABC和Rt△ABD中，
|
∴Rt△ABC≌Rt△ABD（HL），
∴∠CAB=∠DAB，
在△ACE和△ADE中，
|
∴△ACE≌△ADE，
∴∠CEA=∠DEA．
点评：此题考查三角形全等的判定与性质，结合图形，掌握基本的判定方法是解决问题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
在
，-
，
，π，这四个数中，无理数有（ ）
| 22 |
| 7 |
| 3 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
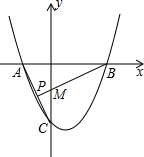如图，抛物线y=x2-bx+c（c＜0）与x轴交于A（-1，0），B两点，与y轴交于点C，AC=
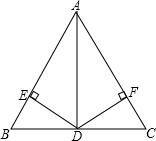如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，BE=CF，∠BAD=18°，求：∠CAD的度数．
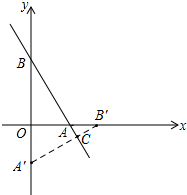如图，直线l：y=-