题目内容
17.某学校利用寒假组织340名师生进行社会实践活动,带有行李170件,计划租用甲、乙两种型号的汽车10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.(1)请你帮助学校设计所有可行的租车方案;
(2)如果甲车的租金为每辆2000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省?
分析 (1)根据甲种汽车x辆,乙种汽车(10-x)辆,甲种汽车每辆最多能载40人和16件行李,乙种汽车每辆最多能载30人和20件行李,列出不等式组,求出x的取值范围,再根据x为正整数,即可得出租车方案;
(2)根据(2)得出的租车方案,再根据甲、乙两种汽车每辆租车费分别为2000元和1800元,即可得出每一种租车的费用,再进行比较,即可得出最省钱的租车方案.
解答 解:(1)设租用甲种汽车x辆,租用乙种汽车(10-x)辆.根据题意得:
$\left\{\begin{array}{l}{40x+30(10-x)≥340}\\{16x+20(10-x)≥170}\end{array}\right.$,
解得:4≤x≤7.5,
∵x为正整数,
∴x可以取4,5,6,7,
∴共有4种租车方案:
方案一:租甲种汽车4辆,租乙种汽车6辆;
方案二:租甲种汽车5辆,租乙种汽车5辆;
方案三:租甲种汽车6辆,租乙种汽车4辆;
方案四:租甲种汽车7辆,租乙种汽车3辆;
(2)方案一的租车费用为:4×2000+6×1800=18800元;
方案二的租车费用为:5×2000+5×1800=19000元;
方案三的租车费用为:6×2000+4×1800=19200元;
方案四的租车费用为:7×2000+3×1800=19400元;
则方案一最省钱.
点评 此题考查了一元一次不等式组的应用,难度一般,解答本题的关键是读懂题意,设出未知数,根据题意的两个不等关系得出不等式组,注意x只能取整数.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
8.下列说法中正确的是( )
| A. | 无理数是无限不循环小数 | B. | 无限小数都是无理数 | ||
| C. | -1的平方根是±1 | D. | -3是9的算术平方根 |
5.一个等腰三角形的两边分别为2cm,5cm,那么这个等腰三角形的( )
| A. | 腰长为2cm | B. | 底长为5cm | C. | 周长为9cm | D. | 周长为12cm |
2.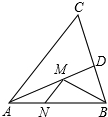 如图,在锐角△ABC中,AB=8,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=8,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
 如图,在锐角△ABC中,AB=8,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=8,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )| A. | 8 | B. | 6 | C. | $4\sqrt{2}$ | D. | $3\sqrt{2}$ |
6.方程(m+2)x|m|+3mx+4=0是关于x的一元二次方程,则( )
| A. | m≠±2 | B. | m=±2 | C. | m=2 | D. | m=-2 |