题目内容
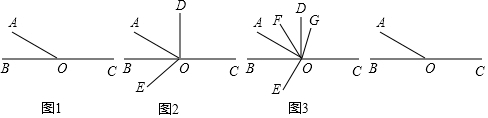
7.如图1,B、O、C在同一条直线上,∠AOB=α(0°<α<60°).(1)若∠BOD=90°,∠AOD=70°,∠AOE=70°,如图2,求∠EOB与∠AOB的比值;
(2)若∠BOD=∠AOE=90°,OF平分∠AOD,OG平分∠AOC,如图3,请比较∠AOF与∠GOC的大小,并求出∠FOG的度数;
(3)若∠AOM与∠AOB互余,∠BON也与∠AOB互余,请直接写出∠MON的度数(用含a的式子表示).
分析 (1)根据角的和差关系可求∠EOB与∠AOB,进一步求得它们的比值;
(2)先根据余角的定义可求∠AOD,再根据角平分线的定义求出∠AOF,先根据补角的定义可求∠AOC,再根据角平分线的定义求出∠FOG,再比较∠AOF与∠GOC的大小,根据角的和差关系可求∠FOG的度数;
(3)分4种情况进行讨论即可求解.
解答 解:(1)∵∠BOD=90°,∠AOD=70°,
∴∠AOB,90°-70°=20°,
∵∠AOE=70°,
∴∠EOB=70°-20°=50°,
∠EOB与∠AOB的比值;
(2)∵∠BOD=∠AOE=90°,
∴∠AOD=90°-α,
∵OF平分∠AOD,
∴∠AOF=$\frac{1}{2}$(90°-α),
∵∠AOC=180°-α,
∵OG平分∠AOC,
∴∠FOG=$\frac{1}{2}$(180°-α),
∴∠AOF<∠GOC,
∴∠FOG=180°-α-$\frac{1}{2}$(90°-α)-$\frac{1}{2}$(180°-α)=45°;
(3)∵∠AOM与∠AOB互余,∠BON也与∠AOB互余,
∴∠AOM=90°-α,∠BON=90°-α,
如图①,∠MON=90°-(90°-α)=α;
如图②,∠MON=90°+(90°-α)=180°-α;
如图③,∠MON=(90°-α-α)+(90°-α)=180°-3α;
如图④,∠MON=(90°-α)-(90°-α-α)=α.
故∠MON的度数为α或180°-α或180°-3α.
点评 本题考查的是邻补角、余角和补角的概念,掌握角平分线的定义是解题的关键.

练习册系列答案
相关题目
17.已知y是x的一次函数,下表中给出了x与y的部分对应值,则m的值是-9.
| x | -1 | 2 | 6 |
| y | 5 | -1 | m |
18. 一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )
一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )
 一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )
一个长方体盒子的长、宽、高分别为3cm,3cm,5cm,一只蚂蚁从盒底的点A沿盒的表面爬到盒顶的点B,蚂蚁爬行的最短路程是( )| A. | $\sqrt{73}$cm | B. | 3$\sqrt{6}$cm | C. | $\sqrt{61}$cm | D. | $\sqrt{53}$cm |
15.下列方程中,解是x=3的是( )
| A. | 3x=1 | B. | 2x-6=0 | C. | 3x+9=0 | D. | $\frac{1}{3}$x=0 |
12.如果$\frac{y}{x}$=2017,则$\frac{y-x}{-x}$等于( )
| A. | 2017 | B. | -2017 | C. | 2016 | D. | -2016 |